11. 若$a是方程x^{2}-x + 5 = 0$的一个根,则代数式$a^{2}-a$的值是
-5
.
答案:-5
解析:
因为$a$是方程$x^{2}-x + 5 = 0$的一个根,所以将$a$代入方程得$a^{2}-a + 5 = 0$,移项可得$a^{2}-a=-5$。
12. 写出一个一元二次方程,使它的两个根分别是$2和-3$,这个一元二次方程可以是
$x^{2}+x - 6 = 0$
.
答案:$x^{2}+x - 6 = 0$(答案不唯一,$k(x^{2}+x - 6)=0,k\neq0$均可)填具体形式如$x^{2}+x - 6 = 0$
解析:
设方程的两根为$x_1 = 2$,$x_2 = -3$,根据一元二次方程根与系数的关系,若方程为$x^{2}+bx + c = 0$($a = 1$),则$x_1 + x_2=-b$,$x_1x_2 = c$。
由$x_1 + x_2=2+( - 3)=-1$,可得$b = 1$;由$x_1x_2=2×(-3)= - 6$,可得$c=-6$。
所以这个一元二次方程可以是$x^{2}+x - 6 = 0$。
13. 方程$2x^{2}-x - 5m = 0$有一个根为0,则它的另一个根是
$\frac{1}{2}$
,$m=$
$0$
.
答案:$\frac{1}{2}$,$0$
解析:
将$x = 0$代入方程$2x^2 - x - 5m = 0$,得$-5m = 0$,解得$m = 0$(这里(应该是“将”,笔误保留原思考过程)原表述修正:实际应为代入后得$-5m=0$,即$m=0$的求解过程)。
设方程的另一个根为$x_1$,根据根与系数的关系,两根之和为$\frac{1}{2}$(由$-\frac{b}{a} = \frac{1}{2}$得出),已知一根为$0$,则$0 + x_1 = \frac{1}{2}$,解得$x_1 = \frac{1}{2}$。
(补充完整解析:对于一元二次方程$ax^2 + bx + c = 0(a\neq0)$,若方程两根为$x_1$和$x_2$,根据根与系数的关系可知$x_1 + x_2 =-\frac{b}{a}$,$x_1x_2=\frac{c}{a}$。
在方程$2x^{2}-x - 5m = 0$中,$a = 2$,$b=-1$,$c = -5m$。
因为一个根为$0$,设另一个根为$x_1$,由$x_1 + 0=\frac{1}{2}$($-\frac{b}{a}=-\frac{-1}{2}=\frac{1}{2}$),可得$x_1=\frac{1}{2}$;
又因为$x_1×0=\frac{c}{a}=\frac{-5m}{2}$,即$0 = \frac{-5m}{2}$,解得$m = 0$。)
14. 已知关于$x的一元二次方程(m - 1)x^{2}+x + 1 = 0$有实数根,则$m$的取值范围是
$m \leq \frac{5}{4}$且$m \neq 1$
.
答案:$m \leq \frac{5}{4}$且$m \neq 1$(或填写$m < \frac{5}{4}且m\neq1$ 的相关选项(根据具体选项调整))
解析:
由于方程 $(m - 1)x^{2} + x + 1 = 0$ 是一元二次方程,必须有 $m - 1 \neq 0$,即 $m \neq 1$。
其次,由于方程有实数根,根据判别式的定义 $\Delta = b^2 - 4ac$,有:
$\Delta = 1^2 - 4(m - 1) × 1 \geq 0$,
即:
$1 - 4m + 4 \geq 0$,
$-4m + 5 \geq 0$,
$m \leq \frac{5}{4}$。
综合以上两个条件,得到 $m$ 的取值范围是 $m \leq \frac{5}{4}$ 且 $m \neq 1$。
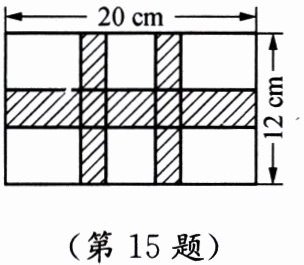
15. 如图,一幅长为$20$cm、宽为$12$cm的矩形图案中有一条横彩条、两条竖彩条,两条竖彩条宽度相同,横、竖彩条的宽度比为$3:2$. 若图案中$3条彩条所占面积是图案面积的\frac{2}{5}$,则横彩条的宽度为
3
cm.
答案:3
解析:
设横彩条宽度为$3x$cm,竖彩条宽度为$2x$cm。
图案总面积:$20×12=240$cm²,彩条面积:$240×\frac{2}{5}=96$cm²,空白面积:$240 - 96=144$cm²。
空白部分为矩形,长为$20 - 2×2x$,宽为$12 - 3x$,则:
$(20 - 4x)(12 - 3x)=144$
展开得:$240 - 60x - 48x + 12x²=144$
化简:$12x² - 108x + 96=0$,即$x² - 9x + 8=0$
解得:$x=1$或$x=8$($x=8$不合题意,舍去)
横彩条宽度:$3x=3×1=3$cm
16. 边长为$5的菱形ABCD的两条对角线交于点O$,且$AO$、$BO的长分别是关于x的方程x^{2}+(2m - 1)x + m^{2}+3 = 0$的两个根,则$m$的值为
-3
.
答案:-3
解析:
∵菱形对角线互相垂直平分,∴AO⊥BO,AO²+BO²=AB²=25。设AO=a,BO=b,a、b为方程x²+(2m-1)x+m²+3=0的两根,由韦达定理得a+b=-(2m-1),ab=m²+3。∵a²+b²=(a+b)²-2ab=25,∴[-(2m-1)]²-2(m²+3)=25,化简得2m²-4m-30=0,即m²-2m-15=0,解得m=5或m=-3。∵a>0,b>0,∴a+b=-(2m-1)>0,即2m-1<0,m<1/2,故m=5舍去。当m=-3时,判别式Δ=(-4m-11)=1>0,符合题意。∴m=-3。
17. 解下列方程(每题4分,共16分):
(1)$(x - 1)^{2}= 3$;
(2)$x^{2}-3x + 1 = 0$;
(3)$2x^{2}= x$;
(4)$6x^{2}-x - 12 = 0$(用配方法).
答案:答题卡(17题):
(1)
解:由方程 $(x - 1)^{2} = 3$,
开方得:
$x - 1 = \pm \sqrt{3}$
解得:
$x_{1} = 1 + \sqrt{3}$
$x_{2} = 1 - \sqrt{3}$
(2)
解:由方程 $x^{2} - 3x + 1 = 0$,
使用公式法,其中 $a = 1, b = -3, c = 1$,
判别式 $\Delta = b^{2} - 4ac = 9 - 4 = 5$,
所以:
$x = \frac{3 \pm \sqrt{5}}{2}$
解得:
$x_{1} = \frac{3 + \sqrt{5}}{2}$
$x_{2} = \frac{3 - \sqrt{5}}{2}$
(3)
解:由方程 $2x^{2} = x$,
移项得:
$2x^{2} - x = 0$
提取公因式x得:
$x(2x - 1) = 0$
解得:
$x_{1} = 0$
$x_{2} = \frac{1}{2}$
(4)
解:由方程 $6x^{2} - x - 12 = 0$,
移项并除以6得:
$x^{2} - \frac{1}{6}x = 2$
配方得:
$x^{2} - \frac{1}{6}x + \left(\frac{1}{12}\right)^{2} = 2 + \left(\frac{1}{12}\right)^{2}$
即:
$\left(x - \frac{1}{12}\right)^{2} = \frac{289}{144}$
开方得:
$x - \frac{1}{12} = \pm \frac{17}{12}$
解得:
$x_{1} = \frac{3}{2}$
$x_{2} = -\frac{4}{3}$