2. 一个长方体,如果长减少2cm,宽和高都不变,那么它的体积减少$48cm^3;$如果宽增加3cm,长和高都不变,那么它的体积增加$99cm^3;$如果高增加4cm,长和宽都不变,那么它的体积增加$352cm^3。$原来长方体的表面积是多少平方厘米?
答案:48÷2 = 24(cm²)
99÷3 = 33(cm²)
352÷4 = 88(cm²)
(24 + 33 + 88)×2 = 290(cm²)
【提示】根据长减少2cm,宽和高都不变,体积减少48cm³,用减少的体积除以减少的长即得左面或右面的面积。用同样的方法可以求出前面或后面、上面或下面的面积。
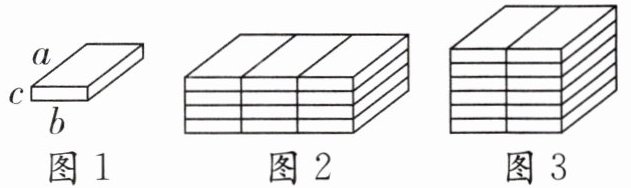
例2 如果把12件同样的长方体物品打包,形成一件大的包装物。下面图2、图3两种打包方式,哪种打包方法物品的表面积较小?(a>b>c)
答案:解析:
本题考查长方体表面积的计算,以及通过比较不同打包方式下大长方体表面积大小,判断哪种打包方式表面积最小,涉及到对长方体表面积公式的运用和根据字母取值范围进行大小比较的知识点。
计算图 2“$3×4$”打包方式的大长方体表面积:
将 12 个小长方体按“$3×4$”的方式打包,此时大长方体的长为$4b$,宽为$3c$,高为$a$。
根据长方体表面积公式$S=(长×宽 + 长×高 + 宽×高)×2$,可得其表面积为:
$\;\;\;\;2(a×3c + a×4b + 3c×4b)$
$= 2(3ac + 4ab + 12bc)$
$= 6ac + 8ab + 24bc$
$= 6ab + 8ac + 24bc$(通过交换律调整顺序,方便后续比较)
计算图 3“$2×6$”打包方式的大长方体表面积:
将 12 个小长方体按“$2×6$”的方式打包,此时大长方体的长为$6b$,宽为$2c$,高为$a$。
同样根据长方体表面积公式,可得其表面积为:
$\;\;\;\;2(a×2c + a×6b + 2c×6b)$
$= 2(2ac + 6ab + 12bc)$
$= 4ac + 12ab + 24bc$
$= 4ab + 12ac + 24bc$(通过交换律调整顺序,方便后续比较)
比较两种打包方式的表面积大小:
用图 2 的表面积减去图 3 的表面积:
$(6ab + 8ac + 24bc) - (4ab + 12ac + 24bc)$
$= 6ab + 8ac + 24bc - 4ab - 12ac - 24bc$
$= 2ab - 4ac$
分情况讨论:
当$2ab - 4ac = 0$,即$2ab = 4ac$,$b = 2c$时,两种打包方法表面积相同。
当$2ab - 4ac< 0$,即$2ab< 4ac$,$b< 2c$时,图 2“$3×4$”的打包方法表面积最小。
当$2ab - 4ac> 0$,即$2ab> 4ac$,$b> 2c$时,图 3“$2×6$”的打包方法表面积最小。
答案:
当$b = 2c$时,两种打包方法表面积相同;当$b< 2c$时,图 2“$3×4$”的打包方法表面积最小;当$b> 2c$时,图 3“$2×6$”的打包方法表面积最小。
3. 一块肥皂的形状是长方体,它的长是9厘米,宽是5厘米,高是2厘米。把10块这样的肥皂包装在一起形成一个大长方体,至少需要多少平方厘米包装纸?(包装纸的重叠部分忽略不计)
答案:包装成长为9厘米、宽和高都为10厘米的大长方体时最省包装纸。
10×10×2 + 9×10×4 = 560(平方厘米)
【提示】将几个完全一样的长方体拼成一个更大的长方体,要想表面积最小,必须尽可能将较大的面重叠在一起。
4. 一个小礼品盒的形状是长9厘米、宽6厘米、高4厘米的长方体。请你帮厂家设计一个能装10个小礼品盒的大纸箱,你觉得怎样设计比较合理?为什么?(纸箱厚度忽略不计)
答案:“2×5”的包法:尽可能让较大面重合,可以叠成一个长为9厘米、宽为12厘米、高为20厘米的长方体,它的表面积为(9×12 + 9×20 + 12×20)×2 = 1056(平方厘米)。
“1×10”的包法:把10个小礼品盒叠在一起,叠成一个长为9厘米、宽为6厘米、高为40厘米的长方体,表面积为(9×6 + 9×40 + 6×40)×2 = 1308(平方厘米)。
【提示】将几个完全一样的长方体拼成一个更大的长方体,要想表面积最小,必须尽可能将大的面积拼接在一起。在设计时,既要考虑到节省材料,又要考虑到美观实用,因此设计一个长为9厘米、宽为12厘米、高为20厘米的长方体纸箱比较合理。
例3 一个长方体容器,从里面量,底面是一个边长为60厘米的正方形,容器里直立着一根高1米的长方体铁棒,其底面是边长为15厘米的正方形,这时容器里的水深50厘米(如图1)。现在把铁棒轻轻地向上提起24厘米(如图2),露出水面的铁棒上被水浸湿的部分长多少厘米?

答案:解析:本题考查长方体体积的计算。
提起那部分铁棒的体积:
$V = 15 × 15 × 24 = 5400$ (立方厘米),
容器的底面积减去铁棒的底面积:
$S = 60 × 60 - 15 × 15 = 3600 - 225 = 3375$ (平方厘米),
水面下降的高度:
$h = \frac{V}{S} = \frac{5400}{3375} = 1.6$ (厘米),
露出水面的铁棒上被水浸湿的部分长度:
$24 + 1.6 = 25.6$ (厘米)。
答案:25.6厘米。