7. 下图是由
18
个棱长1分米的小正方体摆成的,体积是
18
立方分米。不移动现有的小正方体,至少再添上
46
个小正方体,才能摆成一个大正方体。
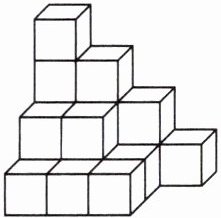
答案:18 18 46 【提示】图中一共有1 + 2 + 5 + 10 = 18(个)小正方体,至少再添上4×4×4 - 18 = 46(个)小正方体才能摆成一个大正方体。
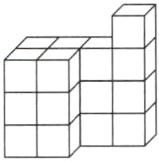
8. 用一些体积是1立方分米的小正方体摆成一个立体图形,分别从这个立体图形的上面、前面和右面看到的形状如下图。这个立体图形中最多有多少个小正方体?

答案:最多有19个小正方体。
【提示】根据从上面看到的形状,可知底面要摆6个小正方体;根据从前面看到的形状,可知在有底面的情况下至少要再添加9个小正方体;再根据从右面看到的形状,且不改变从上面和前面看到的形状,则这时最多只能添加4个小正方体,所以最多有19个小正方体。组成的立体图形如下:
例1 一个长方体,如果长增加3cm,宽和高不变;或者宽增加4cm,长和高不变;或者高增加5cm,长和宽不变,那么它的体积都增加$60cm^3。$这个长方体原来的表面积是多少平方厘米?
答案:解析:
本题考查的是对长方体表面积和体积的综合运用能力。
由题意可知,增加部分的体积分别为:
$3 × \text{宽} × \text{高} = 60 \text{cm}^3$,
$\text{长} × 4 × \text{高} = 60 \text{cm}^3$,
$\text{长} × \text{宽} × 5 = 60 \text{cm}^3$。
从而可得:
$\text{宽} × \text{高} = 20 \text{cm}^2$,
$\text{长} × \text{高} = 15 \text{cm}^2$,
$\text{长} × \text{宽} = 12 \text{cm}^2$。
再代入长方体表面积公式即可求解。
解答:
$60 ÷ 3 = 20 \text{cm}^2$
$60 ÷ 4 = 15 \text{cm}^2$
$60 ÷ 5 = 12 \text{cm}^2$
表面积:
$(12 + 15 + 20) × 2 = 94 \text{cm}^2$
答:这个长方体原来的表面积是 $94 \text{cm}^2$。
1. 如右下图,长方体的长为12cm,高为8cm,涂色部分的两个面的面积和是$200cm^2。$这个长方体的体积是多少立方厘米?

答案:200÷(12 + 8) = 10(cm)
12×8×10 = 960(cm³)
【提示】将涂色部分的两个面平铺就是一个长为12 + 8 = 20(cm)、宽为长方体的宽的长方形,根据“面积÷长=宽”可求长方体的宽,长方体的长和高已知,可求体积。