11. 周末,小亮一家三口开轿车去看望爷爷奶奶和外公外婆.早上从家里出发,向南走了2 km到超市买东西,然后继续向南走了5 km到爷爷家.下午从爷爷家出发向北走了16 km到达外公家,傍晚返回自己家中.
(1)若以小亮家为原点,向南为正方向,用1个单位长度表示2 km,请画出数轴,并将超市、爷爷家、外公家的位置在数轴上分别用A,B,C表示出来.
(2)外公家与超市间的距离为多少千米?
(3)若轿车每千米耗油0.1 L,求小亮一家从早上出发到傍晚返回家中轿车所行路程的耗油量.
答案:(1)由题意得点A,B,C在数轴上表示的数分别为1,3.5,-4.5,如图所示:-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 (2)根据数轴可知外公家与超市间的距离为11km. (3)小亮一家走的路程为2+5+16+9=32(km),共耗油0.1×32=3.2(L).
解析:
(1) 以小亮家为原点,向南为正方向,1个单位长度表示2 km。
超市位置:向南2 km,对应数轴上的数为 $2 ÷ 2 = 1$,记为A;
爷爷家位置:从超市继续向南5 km,共向南 $2 + 5 = 7$ km,对应数轴上的数为 $7 ÷ 2 = 3.5$,记为B;
外公家位置:从爷爷家向北16 km,实际位置为向南 $7 - 16 = -9$ km,对应数轴上的数为 $-9 ÷ 2 = -4.5$,记为C。
数轴如下:
```
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5
C A B
```
(2) 超市A在数轴上的数为1,外公家C在数轴上的数为-4.5,距离为 $|1 - (-4.5)| = 5.5$ 单位长度,实际距离为 $5.5 × 2 = 11$ km。
(3) 总路程:早上从家到超市2 km,超市到爷爷家5 km,下午爷爷家到外公家16 km,傍晚外公家返回家中9 km(外公家在向北9 km处),总路程为 $2 + 5 + 16 + 9 = 32$ km。
耗油量:$32 × 0.1 = 3.2$ L。
答案:(1) 见上述数轴;(2) 11 km;(3) 3.2 L。
12. 新考法 一把刻度尺在数轴上的位置摆放如图①所示,刻度尺右端点B的刻度为“0”,刻度“10 cm”和“25 cm”分别与数轴上表示数0和-2的点重合,现将该刻度尺沿数轴向右平移4个单位长度,如图②,使刻度尺的左端点A与数轴上表示的数1重合,则该刻度尺的长度为______cm.
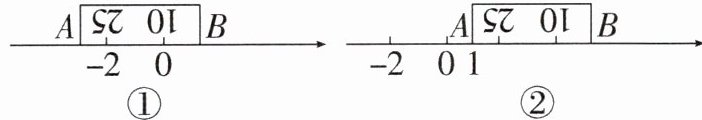
32.5
答案:32.5 解析:因为刻度“10cm”和“25cm”分别与数轴上表示数0 和-2的点重合,所以数轴上一个单位长度表示(25-10)÷2=7.5(cm),将该刻度尺沿数轴向右平移4个单位长度,使刻度尺的左端点A与数轴上表示的数1重合,因此把数1向左平移4个单位长度即是原来点A对应的数-3,原来点A到原点的距离为3×7.5=22.5(cm),所以刻度尺长为22.5+10=32.5(cm).
13. 如图,半径为1个单位长度的圆片上有一点Q与数轴上的原点重合.

(1)把圆片沿数轴向右无滑动的滚动1周,点Q到达数轴上点A的位置,点A表示的数是
2π
.
(2)把圆片沿数轴按同一方向无滑动的滚动2周,点Q到达数轴上点B的位置,点B表示的数是
4π或-4π
.
(3)圆片在数轴上向右无滑动地滚动的周数记为正数,圆片在数轴上向左无滑动地滚动的周数记为负数,依次运动情况记录如下:+2,-1,+3,-6,-1.
①第几次滚动后,点Q距离原点最近? 第几次滚动后,点Q距离原点最远?
②当圆片结束运动时,点Q运动的路程共有多少? 此时点Q所表示的数是多少?
①第2次滚动后,点Q距离原点最近;第3次滚动后,点Q距离原点最远。②点Q运动的路程共有26π,此时点Q所表示的数是-6π。
答案:(1)2π (2)4π或-4π (3)①因为圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左无滑动滚动的周数记为负数,依次运动情况记录如下:+2,-1,+3,-6,-1,所以第1次向右无滑动地滚动2周,点Q到达数4π表示的点;第2次向左无滑动地滚动1周,点Q到达数2π表示的点;第3次向右无滑动地滚动3周,点Q到达数8π表示的点;第4次向左无滑动地滚动6周,点Q到达数-4π表示的点;第5次向左无滑动地滚动1周,点Q到达数-6π表示的点,所以第2次无滑动地滚动后,点Q距离原点最近,第3次无滑动地滚动后,点Q 距离原点最远.②圆片一共无滑动地滚动了2+1+3+6+1=13(周),所以点Q运动的路程共有13×2π×1=26π,由①得此时点Q所表示的数是-6π.
解析:
(1) $2\pi$
(2) $4\pi$ 或 $-4\pi$
(3) ①
第1次滚动后点Q表示的数:$2×2\pi = 4\pi$
第2次滚动后点Q表示的数:$4\pi - 2\pi = 2\pi$
第3次滚动后点Q表示的数:$2\pi + 3×2\pi = 8\pi$
第4次滚动后点Q表示的数:$8\pi - 6×2\pi = -4\pi$
第5次滚动后点Q表示的数:$-4\pi - 2\pi = -6\pi$
距离原点最近的是第2次,最远的是第3次。
②
总滚动周数:$2 + 1 + 3 + 6 + 1 = 13$(周)
运动路程:$13×2\pi×1 = 26\pi$
结束时Q表示的数:$-6\pi$