1. 数学课上老师让同学们画出数轴,下列作图表示数轴正确的是 (
D
)
答案:D
解析:
要判断哪个选项是正确的数轴,需依据数轴的三要素:原点、正方向和单位长度。
选项A:没有原点,不满足数轴三要素,所以A错误。
选项B:没有正方向,不满足数轴三要素,所以B错误。
选项C:数字顺序错误,左边的数应小于右边的数,而这里-1在-2的左边,不符合数轴上数的排列规律,所以C错误。
选项D:有原点(0),规定了向右为正方向,且单位长度统一,满足数轴的三要素,所以D正确。
答案:D
2. (2025·金华期中)如图,在数轴上,手掌遮挡住的点表示的数可能是 (
B
)
A.0.4
B.-0.4
C.-1.4
D.-2.4
答案:B
解析:
由数轴可知,手掌遮挡的点在-1和0之间。
A. 0.4在0和1之间,不符合。
B. -0.4在-1和0之间,符合。
C. -1.4在-2和-1之间,不符合。
D. -2.4在-3和-2之间,不符合。
答案:B
3. (2024·呼和浩特期中)若数轴上表示-1和3的两点分别是点A和点B,则到点A与点B距离相等的点所表示的数是 (
B
)
A.-1
B.1
C.-2
D.2
答案:B
解析:
解:设到点A与点B距离相等的点所表示的数是x。
点A表示-1,点B表示3,根据题意得:|x - (-1)| = |x - 3|
即|x + 1| = |x - 3|
当x + 1 = x - 3时,方程无解;
当x + 1 = -(x - 3)时,x + 1 = -x + 3,2x = 2,x = 1。
答案:B
4. 观察数轴,在-2与3之间(不包括-2与3)的整数有
-1,0,1,2
,有理数有
无数
个.
答案:-1,0,1,$\frac{1}{2}$,2.无数
5. (1)在数轴上点A表示的数为-2,若一个点从A处先向左移动4个单位长度,再向右移动1个单位长度,此时终点所表示的数为
-5
.
(2)(乐山中考改编)数轴上点A表示的数是-3,将点A在数轴上平移7个单位长度得到点B,则点B表示的数是
4或-10
.
答案:(1)-5 (2)4或-10
解析:
(1) 解:点A表示的数为-2,向左移动4个单位长度后表示的数为-2 - 4 = -6,再向右移动1个单位长度后表示的数为-6 + 1 = -5。故答案为-5。
(2) 解:点A表示的数是-3,若向右平移7个单位长度,点B表示的数是-3 + 7 = 4;若向左平移7个单位长度,点B表示的数是-3 - 7 = -10。故答案为4或-10。
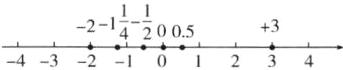
6. 教材P17例2变式 在数轴上画出表示下列各数的点$.+3,-2,0.5,0,-1\frac{1}{4},-\frac{1}{2}.$
答案:如图所示:
7. 数轴上表示整数的点称为整点.某数轴的单位长度为1 cm,若在这条数轴上任意画一条长1 000 cm的线段,则线段盖住的整数点的个数是 (
C
)
A.1 000
B.1 001
C.1 000或1 001
D.999或1 000
答案:C 解析:①当线段的一个端点与数轴上的一个整数点重合时,因为线段长1000cm,所以线段的另一个端点也与数轴上的一个整数点重合,此时线段盖住的整数点的个数是1001;②当线段的一个端点不与数轴上的整数点重合时,线段的另一个端点也不与数轴上的整数点重合,此时线段盖住的整数点的个数是1000.故选C.
8. (2025·遵义期末)如图,等边三角形ABC的边AC在数轴上,现将等边三角形ABC沿着数轴向右翻滚(无滑动),第1次翻滚后点B到点B'位置.若点A表示的数为-1,等边三角形ABC的边长为2,则翻滚2 025次后点A在数轴上对应的数为 (
C
)
A.2 025
B.4 047
C.4 049
D.6 071
答案:C 解析:由题意可得,每3次翻滚为一个循环组依次循环,因为2025÷3=675,所以翻滚2025次后点A在数轴上,所以点A对应的数是-1+675×6=4049.故选C.
9. 如图所示,在数轴上有三个点A,B,C,它们所表示的数分别为-3,-2,2,试回答下列问题.

(1)A,C两点间的距离是
5
;
(2)若点E与点B的距离是8,则点E表示的数是
6或-10
;
(3)若将数轴折叠,使点A与点C重合,则点B与数
1
表示的点重合.
答案:(1)5 (2)6或-10 (3)1 解析:点A与点C重合,则对称轴与数轴的交点到点A和点C的距离相等,它表示的数是-0.5,则点B与数1表示的点重合.
解析:
(1) $|-3 - 2| = 5$
(2) 设点E表示的数为x,$|x - (-2)| = 8$,即$|x + 2| = 8$
当$x + 2 = 8$时,$x = 6$;当$x + 2 = -8$时,$x = -10$
6或-10
(3) 点A与点C重合,对称点表示的数为$\frac{-3 + 2}{2} = -0.5$
设与点B重合的点表示的数为y,$\frac{-2 + y}{2} = -0.5$,解得$y = 1$
1
10. 在数轴上,点A,B在原点O的两侧,分别表示数a,2,将点A向右移动1个单位长度得到点C,若点B与点C到原点的距离相等,则a的值为
-3
.
答案:-3 解析:因为点B表示数2,点A在原点另一侧,所以a<0.又因为点B与点C到原点的距离相等,所以点C表示的数是-2.而点C 是由点A向右移动1个单位长度得到的,反过来将点C向左移动1个单位长度就得到点A,所以点A表示的数a为-3.
解析:
解:因为点A,B在原点O的两侧,点B表示数2,所以a<0。
点A向右移动1个单位长度得到点C,则点C表示的数为a+1。
因为点B与点C到原点的距离相等,点B到原点的距离为2,所以点C到原点的距离也为2。
又因为a<0,所以点C在原点左侧,点C表示的数为-2。
则a+1=-2,解得a=-3。
故a的值为-3。