10. (2024·长春校级月考)如图,将一块长方形铁皮的4个角各剪去一个边长为1m的正方形后,剩下的部分刚好能围成一个容积为$15m^3$的无盖长方体盒子,且此盒子底面的长比宽多2m.设该长方体盒子底面的宽为x m.
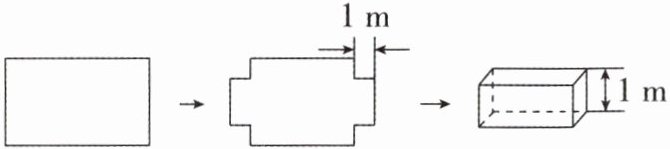
(1)用含x的代数式分别表示出该长方体盒子底面的长和容积;
(2)请根据题意列出关于x的方程.
答案:(1)长方体盒子底面的宽为$x$m,则长为$(x + 2)$m.容积为$x(x + 2)×1 = x(x + 2)m^{3}$. (2)根据题意,得$x(x + 2) = 15$.
解析:
(1)长方体盒子底面的宽为$x\ \text{m}$,则长为$(x + 2)\ \text{m}$。容积为$x(x + 2)×1 = x(x + 2)\ \text{m}^3$。
(2)$x(x + 2) = 15$。
11. 小丽在水果店花18元买了苹果和橘子共6kg,已知苹果每千克3.2元,橘子每千克2.6元.小丽买了苹果和橘子各多少千克?
(1)设所购买的苹果质量为x kg.
①根据“买苹果的金额+买橘子的金额= 18元”,列方程为
3.2x + 2.6(6 - x) = 18
;
②根据“所买苹果的质量+所买橘子的质量= 6kg”,列方程为
x+\frac{18 - 3.2x}{2.6}=6
;
③根据“苹果的单价×其质量= 买苹果的金额”,列方程为
3.2x = 18 - 2.6(6 - x)
.
(2)设买苹果的金额为y元,下列方程正确的是
①③
.(填序号)
①$\frac{y}{3.2} + \frac{18 - y}{2.6} = 6$;
②$y + 2.6(6 - \frac{18 - y}{3.2}) = 18$;
③$3.2(6 - \frac{18 - y}{2.6}) = y$;
④$3.2(6 - \frac{18 - y}{2.6}) = 18 - y$.
答案:(1)①$3.2x + 2.6(6 - x) = 18$ ②$x+\frac{18 - 3.2x}{2.6}=6$③$3.2x = 18 - 2.6(6 - x)$ (2)①③
12. 某校四个班为“希望工程”捐款,甲班捐的钱数是另外三个班捐款总和的一半,乙班捐的钱数是另外三个班捐款总和的$\frac{1}{3}$,丙班捐的钱数是另外三个班捐款总和的$\frac{1}{4}$,丁班共捐了169元,若设这四个班捐款数的总和为x元,请根据条件列出方程:
$x-\frac{1}{3}x-\frac{1}{4}x-\frac{1}{5}x = 169$
.
答案:$x-\frac{1}{3}x-\frac{1}{4}x-\frac{1}{5}x = 169$ 解析:因为甲班捐的钱数是另外三个班捐款总和的一半,所以甲班的捐款数是四个班捐款数总和的$\frac{1}{3}$.因为乙班捐的钱数是另外三个班捐款总和的$\frac{1}{3}$,所以乙班的捐款数是四个班捐款数总和的$\frac{1}{4}$.因为丙班捐的钱数是另外三个班捐款总和的$\frac{1}{4}$,所以丙班的捐款数是四个班捐款数总和的$\frac{1}{5}$.四个班捐款数的总和为$x$元,则甲班捐款$\frac{1}{3}x$元,乙班捐款$\frac{1}{4}x$元,丙班捐款$\frac{1}{5}x$元,根据题意可列出方程为$x-\frac{1}{3}x-\frac{1}{4}x-\frac{1}{5}x = 169$.
解析:
解:设这四个班捐款数的总和为$x$元。
因为甲班捐的钱数是另外三个班捐款总和的一半,所以甲班捐款数占四个班总和的$\frac{1}{1 + 2} = \frac{1}{3}$,即甲班捐款$\frac{1}{3}x$元;
因为乙班捐的钱数是另外三个班捐款总和的$\frac{1}{3}$,所以乙班捐款数占四个班总和的$\frac{1}{1 + 3} = \frac{1}{4}$,即乙班捐款$\frac{1}{4}x$元;
因为丙班捐的钱数是另外三个班捐款总和的$\frac{1}{4}$,所以丙班捐款数占四个班总和的$\frac{1}{1 + 4} = \frac{1}{5}$,即丙班捐款$\frac{1}{5}x$元;
丁班捐款$169$元,根据四个班捐款总和为$x$元,可列方程:$x - \frac{1}{3}x - \frac{1}{4}x - \frac{1}{5}x = 169$。
$x - \frac{1}{3}x - \frac{1}{4}x - \frac{1}{5}x = 169$
13. 新题型 新定义 方程的解的定义:使方程两边相等的未知数的值.如果一个方程的解都是整数,那么这个方程叫作“立信方程”.
(1)若“立信方程”$2x + 1 = 1$的解也是关于x的方程$1 - 2(x - m) = 3$的解,则$m = $
1
;
(2)若关于x的方程$x^{2} + 3x - 4 = 0$的解也是“立信方程”$6x + 2x^{2} - 3 - n = 0$的解,求n的值;
5
(3)关于x的方程$9x - 3 = kx + 14$是“立信方程”,直接写出符合要求的正整数k的值.
8,10,26
答案:(1)1 解析:因为$2x + 1 = 1$,所以$x = 0$,把$x = 0$代入$1 - 2(x - m) = 3$得$1 - 2(0 - m) = 3$,即$1 + 2m = 3$,得$m = 1$. (2)因为$x^{2}+3x - 4 = 0$,所以$x^{2}+3x = 4$,则$2(x^{2}+3x)=2x^{2}+6x = 8$.将$2x^{2}+6x = 8$代入$6x + 2x^{2}-3 - n = 0$,得$8 - 3 - n = 0$,得$n = 5$. (3)符合要求的正整数$k$的值为8,10,26. 解析:由$9x - 3 = kx + 14$得$x=\frac{17}{9 - k}(k\neq9)$,当$9 - k$取$1,-1,17,-17$,即$k$取8,10,-8,26时,$x$的值为整数.所以符合要求的正整数$k$的值为8,10,26.
解析:
(1)解:解方程$2x + 1 = 1$,得$2x=0$,$x = 0$。
把$x = 0$代入$1 - 2(x - m) = 3$,得$1 - 2(0 - m)=3$,即$1 + 2m = 3$,$2m=2$,$m = 1$。
(2)解:解方程$x^{2}+3x - 4 = 0$,因式分解得$(x + 4)(x - 1)=0$,$x + 4 = 0$或$x - 1 = 0$,解得$x=-4$或$x = 1$。
由$x^{2}+3x - 4 = 0$得$x^{2}+3x=4$,则$2x^{2}+6x=8$。
将$2x^{2}+6x = 8$代入$6x + 2x^{2}-3 - n = 0$,得$8 - 3 - n = 0$,$5 - n = 0$,$n = 5$。
(3)8,10,26