1. (青海中考)下列说法中,正确的是 (
C
)
A.若$ac = bc$,则$a = b$
B.若$a^{2} = b^{2}$,则$a = b$
C.若$\frac{a}{c} = \frac{b}{c}$,则$a = b$
D.若$-\frac{1}{3}x = 6$,则$x = 2$
答案:C
解析:
解:A. 若$ac = bc$,当$c = 0$时,$a$不一定等于$b$,故A错误;
B. 若$a^{2} = b^{2}$,则$a = b$或$a=-b$,故B错误;
C. 若$\frac{a}{c} = \frac{b}{c}$,则$c\neq0$,等式两边同乘$c$得$a = b$,故C正确;
D. 若$-\frac{1}{3}x = 6$,等式两边同乘$-3$得$x=-18$,故D错误。
答案:C
2. (2025·大庆校级月考)已知$12x = 4×9$,下面能成立的是 (
A
)
A.$\frac{4}{x} = \frac{12}{9}$
B.$\frac{x}{12} = \frac{4}{9}$
C.$4:x = 9:12$
D.$4x = 12:9$
答案:A
解析:
解:已知$12x = 4×9$,即$12x = 36$,解得$x = 3$。
A. $\frac{4}{x} = \frac{12}{9}$,将$x = 3$代入,左边$\frac{4}{3}$,右边$\frac{12}{9} = \frac{4}{3}$,左边=右边,成立。
B. $\frac{x}{12} = \frac{4}{9}$,代入$x = 3$,左边$\frac{3}{12} = \frac{1}{4}$,右边$\frac{4}{9}$,$\frac{1}{4} ≠ \frac{4}{9}$,不成立。
C. $4:x = 9:12$,根据比例性质$9x = 4×12$,$9x = 48$,$x = \frac{16}{3} ≠ 3$,不成立。
D. $4x = 12:9$,右边$12:9 = \frac{4}{3}$,$4x = \frac{4}{3}$,$x = \frac{1}{3} ≠ 3$,不成立。
答案:A
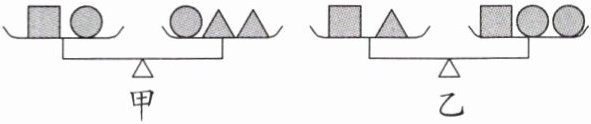
3. (2024·贵州中考)小红学习了等式的基本性质后,在甲、乙两台天平的左右两边分别放入“■”“●”“▲”三种物体,如图所示,天平都保持平衡.若设“■”与“●”的质量分别为$x,y$,则下列关系式正确的是 (
C
)
A.$x = y$
B.$x = 2y$
C.$x = 4y$
D.$x = 5y$
答案:C 解析:设“▲”的质量为a,由甲图可得x + y = y + 2a,即x = 2a,由乙图可得x + a = x + 2y,即a = 2y,所以x = 4y.故选C.
4. (1)已知等式$3x = 2x - 2$,两边同时
减去2x
,得$x = $
-2
,依据是
等式两边都加上(或减去)同一个数或整式,所得结果仍是等式
;
(2)已知等式$-\frac{2}{5}x = \frac{1}{5}$,两边同时
乘$-\frac {5}{2}$(或除以$-\frac {2}{5}$)
,得$x = $
$-\frac {1}{2}$
,依据是
等式两边都乘(或除以)同一个数(除数不能为0),所得结果仍是等式
.
答案:(1)减去2x -2 等式两边都加上(或减去)同一个数或整式,所得结果仍是等式 (2)乘$-\frac {2}{5}$(或除以$-\frac {5}{2}$) $-\frac {1}{2}$ 等式两边都乘(或除以)同一个数(除数不能为0),所得结果仍是等式
5. 根据下列情境中的等量关系列出等式.
(1)$a$的一半比它的3倍少5,用等式表示为
$\frac {1}{2}a=3a-5$
;
(2)一个长方形的周长为26 cm,长方形的长为$x$ cm,如果长减少1 cm,宽增加2 cm,就可成为一个正方形,用等式表示为
$x-1=13-x+2$
;
(3)按如图的方式搭“金鱼”,搭$n$个“金鱼”恰好用了702根小棒,用等式表示为
$2+7n=702$
.
答案:(1)$\frac {1}{2}a=3a-5$ (2)$x-1=13-x+2$ (3)$2+7n=702$
6. (1)已知$2x - 3y + 1 = 0且m - 6x + 9y = 4$,则$m$的值为
1
;
(2)已知$3m^{2} - 2n + 3 = 9$,则$(m^{2} - \frac{2}{3}n + 3)\cdot(6m^{2} - 4n + 3)$的值为
75
.
答案:(1)1 解析:因为2x - 3y + 1 = 0,等式两边同时减去1,得2x - 3y = -1,等式两边同时乘-3,得-6x + 9y = 3,所以m - 6x + 9y = 4,可化为m + 3 = 4,易得m = 1. (2)75 解析:由$3m^{2}-2n+3=9$,得$3m^{2}-2n=6$ ①. ①式两边同时除以3,得$m^{2}-\frac {2}{3}n=2$.①式两边同时乘2,得$6m^{2}-4n=12$.故$(m^{2}-\frac {2}{3}n+3)(6m^{2}-4n+3)=(2+3)×(12+3)=5×15=75$.
解析:
(1)解:因为$2x - 3y + 1 = 0$,所以$2x - 3y = -1$,两边同时乘$-3$得$-6x + 9y = 3$。又因为$m - 6x + 9y = 4$,所以$m + 3 = 4$,解得$m = 1$。
(2)解:由$3m^{2} - 2n + 3 = 9$,得$3m^{2} - 2n = 6$。两边同时除以$3$,得$m^{2} - \frac{2}{3}n = 2$;两边同时乘$2$,得$6m^{2} - 4n = 12$。则$(m^{2} - \frac{2}{3}n + 3)(6m^{2} - 4n + 3) = (2 + 3)×(12 + 3) = 5×15 = 75$。
(1)1;(2)75
7. 教材P108练习T2变式 运用等式的基本性质,将下面的等式变形为$x = c$($c$为常数)的形式:
(1)$7x = 6x - 3$; (2)$-2 = -\frac{1}{2}x$;
(3)$3x - 8 = x$; (4)$7 - \frac{3}{4}x = 4$.
答案:(1)x = -3 (2)x = 4 (3)x = 4 (4)x = 4
解析:
(1)解:7x - 6x = -3
x = -3
(2)解:-2×(-2) = x
x = 4
(3)解:3x - x = 8
2x = 8
x = 4
(4)解:-$\frac{3}{4}$x = 4 - 7
-$\frac{3}{4}$x = -3
x = -3×(-$\frac{4}{3}$)
x = 4
8. (1)已知代数式$3a + 2b与2a + 3b$相等,试用等式的性质比较$a,b$的大小关系;
(2)已知$\frac{1}{2}m - \frac{1}{3}n - 1 = \frac{1}{2}n - \frac{1}{3}m$,试用等式的性质比较$m,n$的大小关系.
答案:(1)由题意得3a + 2b = 2a + 3b,等式两边同时减去(2a + 3b),得3a + 2b - (2a + 3b) = 0,整理得a - b = 0,所以a = b. (2)$\frac {1}{2}m-\frac {1}{3}n-1=\frac {1}{2}n-\frac {1}{3}m$,根据等式的性质可得3m - 2n - 6 = 3n - 2m,整理得5m - 5n = 6,即5(m - n) = 6,故可知$m - n=\frac {6}{5}>0$,所以m > n.