24. (10分)(2025·宿州模拟)项目式学习:探究图式之间的内在联系.
【项目任务】观察下列图形,思考图形中点的排列规律,抽象出数学等式,探究点的总个数.
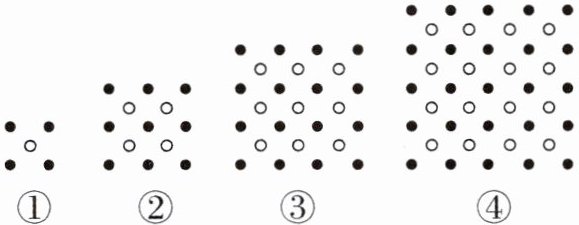
【项目探究过程】下列是三位同学采用不同方法进行探究的过程,请你完善他们的探究过程.
(1)明明同学将这些点分为两类,一类是实心点构造的正方形点阵,一类是空心点构造的正方形点阵,这样图①的点总数可表示为$2^2 + 1^2,$图②的点总数可表示为$3^2 + 2^2,$图③的点总数可表示为$4^2 + 3^2,$图④的点总数可表示为$5^2 + 4^2,…,$图ⓝ的点总数可表示为
$(n + 1)^2 + n^2$
.
(2)欣欣同学用虚线将这些点进行连接,图①的点可以表示为1 + 3 + 1,图②的点可以表示为1 + 3 + 5 + 3 + 1,图③的点可以表示为1 + 3 + 5 + 7 + 5 + 3 + 1,图④的点可以表示为1 + 3 + 5 + 7 + 9 + 7 + 5 + 3 + 1,…,在欣欣思考的这种连接方式下,图ⓝ中最长虚线上共有
$(2n + 1 )$
个点,她结合明明的探究,猜想两种方法利用图ⓝ建立的等式:
$1 + 3 + 5 + \cdots + (2n - 1) + (2n + 1) + (2n - 1) + \cdots + 3 + 1 = (n + 1)^2 + n^2$
,由此获得从1开始,连续n个奇数的和,即1 + 3 + 5 + … + (2n - 1) =
$n^2$
.

(3)慧慧同学在欣欣同学方法的启发下利用这些点构造“回”字图形,结合明明同学的探究,由图①得$1 + 4 = 2^2 + 1^2,$由图②得$1 + 4 + 8 = 3^2 + 2^2,$由图③得$1 + 4 + 8 + 12 = 4^2 + 3^2,…,$利用上述规律计算104 + 108 + 112 + … + 396 + 400的值.

由规律可得$1 + 4 + 8 + 12 + \cdots + 4n = (n + 1)^2 + n^2$,则$1 + 4 + 8 + \cdots + 100 = 26^2 + 25^2$,$1 + 4 + 8 + \cdots + 400 = 101^2 + 100^2$,所以$104 + 108 + 112 + \cdots + 396 + 400 = 101^2 + 100^2 - 26^2 - 25^2 = 18900$。
答案:
(1)$ (n + 1)^2 + n^2 $
(2)$ (2n + 1 ) $ $ 1 + 3 + 5 + \cdots + (2n - 1) + (2n + 1) + (2n - 1) + \cdots + 3 + 1 = (n + 1)^2 + n^2 $ $ n^2 $
(3)由规律可得 $ 1 + 4 + 8 + 12 + \cdots + 4n = (n + 1)^2 + n^2 $, 则 $ 1 + 4 + 8 + \cdots + 100 = 26^2 + 25^2 $, $ 1 + 4 + 8 + \cdots + 400 = 101^2 + 100^2 $, 所以 $ 104 + 108 + 112 + \cdots + 396 + 400 = 101^2 + 100^2 - 26^2 - 25^2 = 18 900 $.
解析:
(1)$(n + 1)^2 + n^2$
(2)$(2n + 1)$;$1 + 3 + 5 + \cdots + (2n - 1) + (2n + 1) + (2n - 1) + \cdots + 3 + 1 = (n + 1)^2 + n^2$;$n^2$
(3)解:由规律可得$1 + 4 + 8 + 12 + \cdots + 4n = (n + 1)^2 + n^2$
因为$4n = 100$时,$n = 25$,所以$1 + 4 + 8 + \cdots + 100 = 26^2 + 25^2$
因为$4n = 400$时,$n = 100$,所以$1 + 4 + 8 + \cdots + 400 = 101^2 + 100^2$
则$104 + 108 + 112 + \cdots + 396 + 400 = (1 + 4 + 8 + \cdots + 400) - (1 + 4 + 8 + \cdots + 100)$
$= 101^2 + 100^2 - 26^2 - 25^2$
$= (10201 + 10000) - (676 + 625)$
$= 20201 - 1301$
$= 18900$
25. (14分)(2025·苏州期中)如图,甲、乙两人(看成点)分别在数轴-14和15的位置上,沿数轴做移动游戏.每次移动游戏规则:两人先进行“石头、剪刀、布”,然后根据输赢结果进行移动.

①若平局,则甲向东移动1个单位长度,同时乙向西移动1个单位长度;
②若甲赢,则甲向东移动3个单位长度,同时乙向东移动1个单位长度;
③若乙赢,则甲向西移动1个单位长度,同时乙向西移动3个单位长度.
(1)从如图的位置开始,若完成了1次移动游戏,甲、乙“石头、剪刀、布”的结果为平局,则移动后甲、乙两人相距
27
个单位长度.
(2)从如图的位置开始,若完成了10次移动游戏,发现甲、乙每次都有输有赢(无平局).设乙赢了n次,且他最终停留的位置对应的数为m,试用含n的式子表示m,并求出该位置距离原点O最近时n的值.
因为乙赢了n次,所以乙输了(10 - n)次。乙赢n次后位置为15 - 3n,输(10 - n)次后位置为15 - 3n + (10 - n),故m = 25 - 4n。当n = 6时,该位置距离原点O最近。
(3)从如图的位置开始,若进行了k次移动游戏后,甲与乙的位置相距3个单位长度,直接写出k的值.
k = 13 或 k = 16
答案:(1)27 解析:完成了 1 次移动游戏, 结果为平局, 则甲向东移动 1 个单位长度到 -13, 乙向西移动 1 个单位长度到 14, 移动后甲、乙两人相距 $ 14 - ( - 13 ) = 27 $ (个) 单位长度. (2) 因为乙赢了 $ n $ 次, 所以乙输了 $ (10 - n) $ 次. 因为若乙赢, 则甲向西移动 1 个单位长度, 同时乙向西移动 3 个单位长度, 所以乙赢了 $ n $ 次后, 乙停留的位置对应的数为 $ 15 - 3n $. 因为若甲赢, 则甲向东移动 3 个单位长度, 同时乙向东移动 1 个单位长度, 所以乙输了 $ (10 - n) $ 次后, 乙停留的位置对应的数为 $ 15 - 3n + (10 - n) $, 根据题意得 $ 15 - 3n + (10 - n) = m $, 所以 $ m = 25 - 4n $. 因为 $ n $ 为正整数, 所以当 $ n = 6 $ 时, 该位置距离原点 $ O $ 最近. (3)$ k = 13 $ 或 $ k = 16 $. 解析:由题意可得刚开始两人的距离为 29, 因为若平局, 则甲向东移动 1 个单位长度, 同时乙向西移动 1 个单位长度, 所以若平局 (甲小于乙), 移动后甲、乙的距离缩小 2 个单位长度. 因为若甲赢, 则甲向东移动 3 个单位长度, 同时乙向东移动 1 个单位长度, 所以若甲赢 (甲小于乙), 移动后甲、乙的距离缩小 2 个单位长度. 因为若乙赢, 则甲向西移动 1 个单位长度, 同时乙向西移动 3 个单位长度, 所以若乙赢 (甲小于乙), 移动后甲、乙的距离缩小 2 个单位长度, 所以甲、乙每移动一次, 甲、乙的距离缩小 2 个单位长度. 因为甲与乙的位置相距 3 个单位长度有两种情况: ①甲与乙的距离缩小 26 个单位长度, 此时 $ k = 26 ÷ 2 = 13 $ (次); ②甲与乙的距离缩小到 0 后又增加到 3 个单位长度, 此时 $ k = (29 + 3) ÷ 2 = 16 $ (次). 综上所述, $ k $ 的值为 13 或 16.
解析:
(1)27
(2)解:因为乙赢了$n$次,所以乙输了$(10 - n)$次。
乙赢$n$次后位置:$15 - 3n$;乙输$(10 - n)$次后位置:$15 - 3n + (10 - n)$。
则$m = 15 - 3n + 10 - n = 25 - 4n$。
当$n = 6$时,$m = 25 - 24 = 1$,距离原点最近。
(3)$k = 13$或$k = 16$