21. (8分)对于有理数a,b,定义一种新运算“⊙”,规定a⊙b = |a + b| + |a - b|.
(1)计算3⊙(-4)的值;
(2)当a,b在数轴上的位置如图所示时,化简a⊙b.
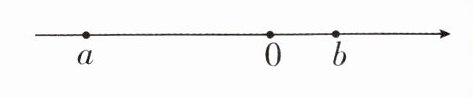
答案:(1)根据题意知 $ 3 \odot ( - 4 ) = | 3 + ( - 4 ) | + | 3 - ( - 4 ) | = 1 + 7 = 8 $. (2) 由题图可知 $ a < 0 < b $, 且 $ | a | > | b | $, 则 $ a + b < 0 $, $ a - b < 0 $. 所以 $ a \odot b = | a + b | + | a - b | = - a - b - a + b = - 2 a $.
解析:
(1) $3 \odot (-4) = |3 + (-4)| + |3 - (-4)| = |-1| + |7| = 1 + 7 = 8$
(2) 由数轴可知 $a < 0 < b$,且 $|a| > |b|$,则 $a + b < 0$,$a - b < 0$
$a \odot b = |a + b| + |a - b| = -(a + b) + -(a - b) = -a - b - a + b = -2a$
22. (8分)小明根据市自来水公司的居民用水收费标准,制定了水费计算数值转换机的示意图.(用水量单位:$m^3,$水费单位:元)

(1)根据转换机程序计算下列各户月应缴纳水费:
|用户|张大爷家|王阿姨家|小明家|
|月用水量$/m^3$|6|15|17|
|月应缴纳水费/元|
18
|
45
|
55
|
(2)当x > 15时,用含x的代数式表示应缴纳水费
(5x - 30)
元;
(3)小丽家10月份缴纳水费70元,则小丽家10月份用水多少立方米?
(70 - 15×3)÷5 + 15 = 20 (m^3) 答: 小丽家 10 月份用水 20 m^3 .
答案:(1)18 45 55 (2)$ (5x - 30) $ (3)$ (70 - 15×3)÷5 + 15 = 20 (m^3) $ 答: 小丽家 10 月份用水 $ 20 m^3 $.
解析:
(1)
张大爷家:$6×3 = 18$(元)
王阿姨家:$15×3 = 45$(元)
小明家:$(17 - 15)×5 + 15×3 = 2×5 + 45 = 10 + 45 = 55$(元)
故表格依次填:18;45;55
(2)当$x>15$时,水费为$(x - 15)×5 + 15×3 = 5x - 75 + 45 = 5x - 30$,故填$5x - 30$
(3)解:设小丽家10月份用水$x m^3$。
因为$15×3 = 45$(元),$70>45$,所以$x>15$。
依题意得$5x - 30 = 70$
$5x = 70 + 30$
$5x = 100$
$x = 20$
答:小丽家10月份用水$20 m^3$。
23. (10分)如图是某展馆的平面图,其外框是一个大正方形,中间四个大小相同的小正方形(阴影部分)是绿化区域,标记了字母的五个大小相同的正方形是展厅,剩余的是四个大小相同的休息厅,已知种植绿化的正方形边长比展厅的正方形边长的一半多1m,设展厅的正方形边长为x m.
(1)种植绿化的正方形边长为
$ (\frac{1}{2}x + 1) $
m;(用含x的整式表示)
(2)该展馆的平面图外框大正方形的周长为
$ (16x + 8) $
m,每个休息厅的图形周长为
$ (7x + 6) $
m;(用含x的整式表示)
(3)若设种植绿化的正方形边长为2m,求该展馆的占地面积.
当$ \frac{1}{2}x + 1 = 2 $,即$ x = 2 $时,该展馆的占地面积为$ (4x + 2)^2 = (4×2 + 2)^2 = 100(m^2) $。
答案:(1)$ ( \frac{1}{2}x + 1 ) $ (2)$ (16x + 8 ) $ $ (7x + 6 ) $ 解析:该展馆的平面图外框大正方形的周长为 $ 4 × [ 3 x + 2 ( \frac{1}{2} x + 1 ) ] = ( 16 x + 8 ) $ m, 每个休息厅的图形周长为 $ 2 × [ x + 2 ( \frac{1}{2} x + 1 ) + x + \frac{1}{2} x + 1 ] = ( 7 x + 6 ) $ m. (3) 当 $ \frac{1}{2} x + 1 = 2 $, 即 $ x = 2 $ 时, 该展馆的占地面积为 $ ( 4 x + 2 ) ^ { 2 } = ( 4 × 2 + 2 ) ^ { 2 } = 100 ( m ^ { 2 } ) $.
解析:
(1)$\left(\dfrac{1}{2}x + 1\right)$
(2)$16x + 8$;$7x + 6$
(3)解:当种植绿化的正方形边长为$2\ \text{m}$时,
$\dfrac{1}{2}x + 1 = 2$
解得$x = 2$
大正方形边长为$3x + 2\left(\dfrac{1}{2}x + 1\right)=3×2 + 2×2=10\ \text{m}$
占地面积为$10×10 = 100\ \text{m}^2$
答:该展馆的占地面积为$100\ \text{m}^2$