15. 如图是一个数值运算的程序,若输出y的值为40,则输入的x的值为
9 或 -9
.
答案:9 或 -9
解析:
解:根据程序可得运算式为$y = \frac{x^2 - 1}{2}$。
已知输出$y = 40$,则:
$\frac{x^2 - 1}{2} = 40$
$x^2 - 1 = 80$
$x^2 = 81$
$x = \pm 9$
答案:9 或 -9
16. 如图,在数轴上竖直摆放一个直径为4个单位长度的半圆,A是半圆弧的中点,半圆直径的一个端点位于原点O.该半圆沿数轴从原点O开始向右无滑动滚动,当点A第一次落在数轴上时,此时点A表示的数为
4 + π
.
答案:$ 4 + \pi $
解析:
解:半圆直径为4,半径为2。初始时,半圆直径端点在原点O,A为半圆弧中点,位于直径上方。
半圆无滑动滚动,当A第一次落在数轴上时,半圆需滚动半周。
滚动过程中,圆心水平移动距离等于半圆周长的一半,即$\frac{1}{2} × \pi × 4 = 2\pi$。但此时A点轨迹为以圆心为顶点的圆弧,当滚动半周后,A点从初始位置(圆心正上方)旋转180°至圆心正下方,此时A点到初始原点O的距离为:直径长度(4)加上圆心移动距离的一半(因为滚动半周,圆心移动距离为半圆周长的一半$2\pi$,但此时A点相对于圆心的水平位移为0,水平总距离为初始直径长度4)。
故点A表示的数为$4 + \pi$。
答案:$4 + \pi$
17. 如图,用含a的代数式表示图中阴影部分的面积为
$\frac{1}{2}\pi a^2 - a^2$
.(结果保留π)
答案:$ \frac{1}{2}\pi a^2 - a^2 $ 解析:观察题图可得, 阴影部分的面积等于两个半径为 $ a $ 的四分之一圆的面积的和减去边长为 $ a $ 的正方形的面积, 即阴影部分的面积为 $ 2 × \frac{1}{4} × \pi × a^2 - a^2 = \frac{1}{2}\pi a^2 - a^2 $.
解析:
解:阴影部分的面积为两个半径为 $a$ 的四分之一圆的面积之和减去边长为 $a$ 的正方形的面积。
两个四分之一圆的面积和为:$2×\frac{1}{4}×\pi× a^2=\frac{1}{2}\pi a^2$
正方形的面积为:$a^2$
所以阴影部分面积为:$\frac{1}{2}\pi a^2 - a^2$
$\frac{1}{2}\pi a^2 - a^2$
18. (扬州中考)将黑色圆点按如图所示的规律进行排列:
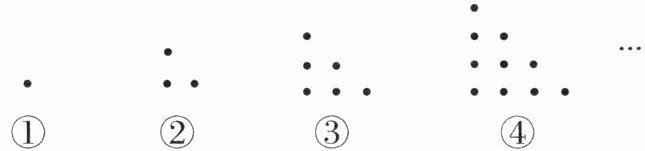
图中黑色圆点的个数依次为1,3,6,10,…,将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据,则新数据中的第33个数为______
1275
.
答案:1 275 解析:题图①②③④中的黑色圆点的个数分别为 1, 3, 6, 10, 所以第 $ n $ 个图形中的黑色圆点的个数为 $ \frac{n(n + 1)}{2} $, 所以这列数为 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, …, 其中每 3 个数中, 后 2 个数能被 3 整除, $ 33 ÷ 2 = 16 \cdots 1 $, $ 16 × 3 + 2 = 50 $, 则第 33 个能被 3 整除的数为原数列中第 50 个数, 即 $ \frac{50 × 51}{2} = 1 275 $. 故答案为 1 275.
解析:
解:第$n$个图形中黑色圆点的个数为$\frac{n(n + 1)}{2}$。
原数列:1,3,6,10,15,21,28,36,45,55,66,78,91,…
观察可知,每3个数中后2个数能被3整除。
$33÷2 = 16\cdots\cdots1$,则原数列中对应的项数为$16×3 + 2=50$。
第50个数为$\frac{50×51}{2}=1275$。
故答案为1275。
$19. (10$分$)$计算:
$(1)(-3) + (-4) - (+11) - (-9);$$(2)-1^{100} + (-\frac{1}{8} + \frac{1}{3} - \frac{1}{6})×(-24);$
$(3)1\frac{1}{2}×\frac{5}{7} - (-\frac{5}{7})×2\frac{1}{2} + (-\frac{1}{2})÷1\frac{2}{5};$$(4)-199\frac{5}{7}×14($要求用简便方法计算$);$$(5)-4^2×\frac{5}{8} - |-5|×(-4)^3×\frac{1}{4} + 2^2÷4.$
答案:
(1)-9
(2)-2
(3)$ \frac{5}{2} $
(4)-2 796
(5)71
解析:
(1)解:原式=-3-4-11+9=-18+9=-9
(2)解:原式$=-1+(-\frac{1}{8})×(-24)+\frac{1}{3}×(-24)-\frac{1}{6}×(-24)=-1+3-8+4=-2$
(3)解:原式$=\frac{3}{2}×\frac{5}{7}+\frac{5}{7}×\frac{5}{2}-\frac{1}{2}×\frac{5}{7}=\frac{5}{7}×(\frac{3}{2}+\frac{5}{2}-\frac{1}{2})=\frac{5}{7}×\frac{7}{2}=\frac{5}{2}$
(4)解:原式$=(-200+\frac{2}{7})×14=-200×14+\frac{2}{7}×14=-2800+4=-2796$
(5)解:原式$=-16×\frac{5}{8}-5×(-64)×\frac{1}{4}+4÷4=-10+80+1=71$
20. (6分)先化简,再求值:$(1)2x^2 - [3(-\frac{1}{3}x^2 + \frac{2}{3}xy) + 2y^2] - 2(x^2 - xy - 2y^2),其中x = \frac{1}{2},$y = -1;
(2)已知a + b = 4,ab = -2,求$(4a - 3b + 2ab) - 2(a - \frac{5}{2}b - ab)$的值.
答案:(1)原式 $ = 2 x ^ { 2 } - ( - x ^ { 2 } + 2 x y + 2 y ^ { 2 } ) - 2 ( x ^ { 2 } - x y - 2 y ^ { 2 } ) = 2 x ^ { 2 } + x ^ { 2 } - 2 x y - 2 y ^ { 2 } - 2 x ^ { 2 } + 2 x y + 4 y ^ { 2 } = x ^ { 2 } + 2 y ^ { 2 } $, 当 $ x = \frac{1}{2} $, $ y = -1 $ 时, 原式 $ = ( \frac{1}{2} ) ^ { 2 } + 2 × ( - 1 ) ^ { 2 } = \frac{1}{4} + 2 = \frac{9}{4} $. (2) $ ( 4 a - 3 b + 2 a b ) - 2 ( a - \frac{5}{2} b - a b ) = 4 a - 3 b + 2 a b - 2 a + 5 b + 2 a b = 2 a + 2 b + 4 a b = 2 ( a + b ) + 4 a b $, 当 $ a + b = 4 $, $ a b = - 2 $ 时, 原式 $ = 2 × 4 + 4 × ( - 2 ) = 0 $.
解析:
(1)解:原式$=2x^2 - [3(-\frac{1}{3}x^2 + \frac{2}{3}xy) + 2y^2] - 2(x^2 - xy - 2y^2)$
$=2x^2 - (-x^2 + 2xy + 2y^2) - 2x^2 + 2xy + 4y^2$
$=2x^2 + x^2 - 2xy - 2y^2 - 2x^2 + 2xy + 4y^2$
$=x^2 + 2y^2$
当$x = \frac{1}{2}$,$y = -1$时,原式$=(\frac{1}{2})^2 + 2×(-1)^2 = \frac{1}{4} + 2 = \frac{9}{4}$
(2)解:$(4a - 3b + 2ab) - 2(a - \frac{5}{2}b - ab)$
$=4a - 3b + 2ab - 2a + 5b + 2ab$
$=2a + 2b + 4ab$
$=2(a + b) + 4ab$
当$a + b = 4$,$ab = -2$时,原式$=2×4 + 4×(-2) = 8 - 8 = 0$