1. 2024年10月30日,神舟十九号载人飞船在酒泉卫星发射中心点火发射.若火箭发射点火前5秒记为-5秒,那么火箭发射点火后10秒应记为(
A
)
A.+10秒
B.-5秒
C.+5秒
D.-10秒
答案:A
解析:
火箭发射点火前记为负,点火后应记为正,点火后10秒记为+10秒。
答案:A
2. 在有理数-0.8,-(+5),0,$3\frac{5}{6},$-|-2|,100中,非负整数有(
B
)
A.1个
B.2个
C.3个
D.4个
答案:B
解析:
解:在有理数-0.8,-(+5),0,$3\frac{5}{6},$-|-2|,100中,
非负整数是指大于等于0的整数,
-(+5)=-5,-|-2|=-2,
所以非负整数有0,100,共2个。
答案:B
3. (2025·高邮期末)对于代数式-1 + k的值,下列说法正确的是(
C
)
A.比-1大
B.比-1小
C.比k小
D.比k大
答案:C
解析:
解:
-1 + k = k - 1
因为 k - 1 < k(减去一个正数,结果比原数小),
所以代数式-1 + k的值比k小。
答案:C
4. 下列说法错误的是(
C
)
$A.2x^2 - 3xy - 1$是二次三项式
B.-x + 1不是单项式
$C.-\frac{\pi}{3}xy^2$的系数是$-\frac{1}{3}$
$D.-2^2xab^2$的次数是4
答案:C
解析:
解:A. $2x^2 - 3xy - 1$是二次三项式,正确;
B. $-x + 1$是多项式,不是单项式,正确;
C. $-\frac{\pi}{3}xy^2$的系数是$-\frac{\pi}{3}$,原说法错误;
D. $-2^2xab^2$的次数是$1+1+2=4$,正确。
结论:C
5. 我国古代数学名著《九章算术》里,记载了利用算筹实施“正负术”的方法,图①表示的是计算3 + (-4)的过程.按照这种方法,图②中表示的式子的计算结果是(
C
)
A.-7
B.-3
C.3
D.7
答案:C
6. 若|m| = 3,|n| = 2,且$\frac{m}{n} < 0,$则m + n的值是(
D
)
A.-1
B.1
C.1或5
D.±1
答案:D
解析:
解:
∵|m|=3,∴m=±3;
∵|n|=2,∴n=±2;
∵$\frac{m}{n}<0$,∴m、n异号。
情况1:m=3,n=-2时,m+n=3+(-2)=1;
情况2:m=-3,n=2时,m+n=-3+2=-1。
综上,m+n的值是±1。
答案:D
7. (2025·厦门期中)如图,M,N,P,R分别是数轴上四个整数m,n,p,r所对应的点,其中有一点是原点,并且r - p = p - n = n - m = 2.数a对应的点在M与N之间,数b对应的点在P与R之间,若|a| + |b| = 6,则原点是(
B
)
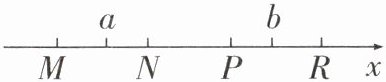
A.M或N
B.M或R
C.N或P
D.P或R
答案:B 解析:因为 $ r - p = p - n = n - m = 2 $, 点 $ M $, $ R $ 之间的距离为 $ 6 $, 设数 $ a $ 对应的点为点 $ A $, 数 $ b $ 对应的点为点 $ B $, ①当原点在 $ N $ 或 $ P $ 点时, $ | a | + | b | < 6 $, 和题意相互矛盾, 故原点不可能在 $ N $ 或 $ P $ 点; ②当原点在 $ M $ 或 $ R $ 点时且 $ | MA | = | BR | $ 时, $ | a | + | b | = 6 $, 故原点应该在 $ M $ 或 $ R $ 点. 故选 B.
8. 把两张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为x cm,宽为y cm)的盒子底部(如图②),盒子底部未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分周长的和是(
D
)

A.2(x + y)cm
B.4(x - y)cm
C.4x cm
D.4y cm
答案:D 解析:设题图①小长方形卡片的长为 $ c $ cm, 宽为 $ n $ cm. 根据题意, 得两块阴影部分的周长和为 $ 2 [ m + ( y - n ) ] + 2 [ n + ( y - m ) ] = 2 ( m + y - n + n - m + y ) = 2 × 2 y = 4 y $ cm. 故选 D.
9. 倒数等于2的数是
$\frac{1}{2}$
,|-3|的相反数是
-3
.
答案:$ \frac { 1 } { 2 } $ -3
10. 比较大小:$-\frac{2}{3}$
>
$-\frac{3}{4}.($用“>”“<”或“=”填空)
答案:>
解析:
解:比较两个负数的大小,先比较它们的绝对值。
$\left| -\frac{2}{3} \right| = \frac{2}{3} = \frac{8}{12}$,$\left| -\frac{3}{4} \right| = \frac{3}{4} = \frac{9}{12}$。
因为$\frac{8}{12} < \frac{9}{12}$,所以$-\frac{2}{3} > -\frac{3}{4}$。
>
11. (2024·上海中考)科学家研发了一种新的蓝光唱片,一张蓝光唱片的容量约为$2×10^5GB,$一张普通唱片的容量约为25GB,则蓝光唱片的容量是普通唱片的______倍.(用科学记数法表示)
$8×10^3$
答案:$ 8×10^3 $
解析:
解:$(2×10^5)÷25 = (2÷25)×10^5 = 0.08×10^5 = 8×10^3$
$8×10^3$
12. 若$7a^xb^2与-3a^3b^y$的和为单项式,则$x^y = $
9
.
答案:9
解析:
解:因为$7a^xb^2$与$-3a^3b^y$的和为单项式,所以它们是同类项。
同类项要求相同字母的指数相同,故$x = 3$,$y = 2$。
则$x^y = 3^2 = 9$。
答案:9
13. (2023·泰州中考)若2a - b + 3 = 0,则2(2a + b) - 4b的值为
-6
.
答案:-6
解析:
解:2(2a + b) - 4b
= 4a + 2b - 4b
= 4a - 2b
= 2(2a - b)
因为2a - b + 3 = 0,所以2a - b = -3
则原式=2×(-3)= -6
答案:-6
14. 小明说:“请你任意想一个数,把这个数乘-3后加12,然后除以6,再加上你原来所想的那个数的一半,我可以知道你计算的结果.”请你写出这个计算结果是
2
.
答案:2
解析:
设原来所想的数为$x$。
根据题意,计算过程为:
$\begin{aligned}&\frac{-3x + 12}{6} + \frac{x}{2}\\=&\frac{-3x}{6} + \frac{12}{6} + \frac{x}{2}\\=&-\frac{x}{2} + 2 + \frac{x}{2}\\=&2\end{aligned}$
结果是$2$。