2025年学霸题中题七年级数学上册苏科版第81页解析答案

9. (2025·连云港期中)如图①,在数轴上点 $ M $ 表示的数为 $ m $,点 $ N $ 表示的数为 $ n $,点 $ M $ 到点 $ N $ 的距离记为 $ MN $。如图②,在数轴上点 $ A $ 表示数 $ a $,点 $ B $ 表示数 $ b $,点 $ C $ 表示数 $ c $,$ b $ 是最大的负整数,且 $ a $,$ c $ 满足 $ ( a + 3 ) ^ { 2 } $ 与 $ | c - 5 | $ 互为相反数。
(1)$ a = $

-3

,$ b = $

-1

,$ c = $

。
(2)点 $ A $,$ B $,$ C $ 开始在数轴上运动,若点 $ A $ 以每秒 $ 2 $ 个单位长度的速度向左运动,同时,点 $ B $ 和点 $ C $ 分别以每秒 $ 1 $ 个单位长度和 $ 3 $ 个单位长度的速度向右运动,假设 $ t $ 秒后。
① 请问：$ 6 B C - 4 A B $ 的值是否随着时间 $ t $ 的变化而改变？若变化,请说明理由；若不变,请求其值。
② 探究：若点 $ A $,$ C $ 向右运动,点 $ B $ 向左运动,速度保持不变,$ 3 B C - 4 A B $ 的值是否随着时间 $ t $ 的变化而改变？若变化,请说明理由；若不变,请求其值。

(2)① $t$ 秒后，$A$ 表示的数为 $-3 - 2t$，$B$ 表示的数为 $-1 + t$，$C$ 表示的数为 $5 + 3t$，所以 $BC = 5 + 3t-(-1 + t)=6 + 2t$，$AB=-1 + t-(-3 - 2t)=2 + 3t$，所以 $6BC - 4AB = 6(6 + 2t)-4(2 + 3t)=36 + 12t - 8 - 12t = 28$，故不变，其值为 28。
② $t$ 秒后，$A$ 表示的数为 $-3 + 2t$，$B$ 表示的数为 $-1 - t$，$C$ 表示的数为 $5 + 3t$，所以 $BC = 5 + 3t-(-1 - t)=6 + 4t$，$AB=|-1 - t-(-3 + 2t)|=|2 - 3t|$，当 $A$，$B$ 重合时，$-3 + 2t=-1 - t$，解得 $t=\frac{2}{3}$，此时 $3BC - 4AB = 26$；当 $A$ 在 $B$ 的左侧，即 $0＜t＜\frac{2}{3}$ 时，$AB = 2 - 3t$，所以 $3BC - 4AB = 3(6 + 4t)-4(2 - 3t)=18 + 12t - 8 + 12t = 10 + 24t$，所以 $3BC - 4AB$ 的值随时间 $t$ 的变化而变化；当 $A$ 在 $B$ 的右侧，即 $t＞\frac{2}{3}$ 时，$AB = 3t - 2$，所以 $3BC - 4AB = 3(6 + 4t)-4(3t - 2)=18 + 12t - 12t + 8 = 26$。综上，当 $0＜t＜\frac{2}{3}$ 时，$3BC - 4AB$ 的值随时间 $t$ 的变化而变化；当 $t\geq\frac{2}{3}$ 时，$3BC - 4AB$ 的值为 26。

答案：(1) -3 -1 5
(2)① $t$ 秒后，$A$ 表示的数为 $-3 - 2t$，$B$ 表示的数为 $-1 + t$，$C$ 表示的数为 $5 + 3t$，所以 $BC = 5 + 3t-(-1 + t)=6 + 2t$，$AB=-1 + t-(-3 - 2t)=2 + 3t$，所以 $6BC - 4AB = 6(6 + 2t)-4(2 + 3t)=36 + 12t - 8 - 12t = 28$，故不变，其值为 28。
② $t$ 秒后，$A$ 表示的数为 $-3 + 2t$，$B$ 表示的数为 $-1 - t$，$C$ 表示的数为 $5 + 3t$，所以 $BC = 5 + 3t-(-1 - t)=6 + 4t$，$AB=|-1 - t-(-3 + 2t)|=|2 - 3t|$，当 $A$，$B$ 重合时，$-3 + 2t=-1 - t$，解得 $t=\frac{2}{3}$，此时 $3BC - 4AB = 26$；当 $A$ 在 $B$ 的左侧，即 $0＜t＜\frac{2}{3}$ 时，$AB = 2 - 3t$，所以 $3BC - 4AB = 3(6 + 4t)-4(2 - 3t)=18 + 12t - 8 + 12t = 10 + 24t$，所以 $3BC - 4AB$ 的值随时间 $t$ 的变化而变化；当 $A$ 在 $B$ 的右侧，即 $t＞\frac{2}{3}$ 时，$AB = 3t - 2$，所以 $3BC - 4AB = 3(6 + 4t)-4(3t - 2)=18 + 12t - 12t + 8 = 26$。综上，当 $0＜t＜\frac{2}{3}$ 时，$3BC - 4AB$ 的值随时间 $t$ 的变化而变化；当 $t\geq\frac{2}{3}$ 时，$3BC - 4AB$ 的值为 26。

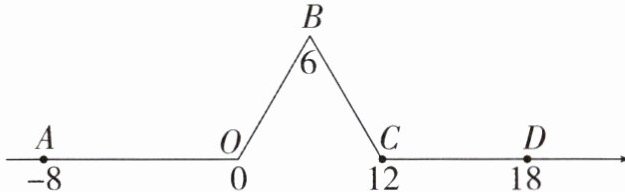
10. (2025·扬州期中)数轴上点 $ A $ 表示 $ - 8 $,点 $ B $ 表示 $ 6 $,点 $ C $ 表示 $ 12 $,点 $ D $ 表示 $ 18 $。如图,将数轴在原点 $ O $ 和点 $ B $,$ C $ 处各折一下,得到一条“折线数轴”。在折线数轴上,把两点所对应的两数之差的绝对值叫这两点间的“和谐距离”。例如,点 $ A $ 和点 $ D $ 在折线数轴上的和谐距离为 $ | - 8 - 18 | = 26 $ 个单位长度,动点 $ M $ 从点 $ A $ 出发,以 $ 4 $ 个单位长度/秒的速度沿着折线数轴的正方向运动,从点 $ O $ 运动到点 $ C $ 期间速度变为原来的一半,过点 $ C $ 后继续以原来的速度向终点 $ D $ 运动,点 $ M $ 从点 $ A $ 出发的同时,点 $ N $ 从点 $ D $ 出发,一直以 $ 3 $ 个单位长度/秒的速度沿着“折线数轴”负方向向终点 $ A $ 运动,其中一点到达终点时,两点都停止运动,设运动的时间为 $ t $ s。
(1)当 $ t = 2 $ s 时,$ M $,$ N $ 两点在折线数轴上的和谐距离 $ | M N | $ 为______

；
(2)当 $ t = $______时,$ M $,$ N $ 两点在折线段 $ O - B - C $ 上相遇

$\frac{22}{5}$

；
(3)当 $ t = $______时,$ M $,$ N $ 两点在折线数轴上的和谐距离为 $ 4 $ 个单位长度

$\frac{18}{5}$ 或 $\frac{26}{5}$

；
(4)当 $ t $ 为几秒时,$ M $,$ O $ 两点在折线数轴上的和谐距离与 $ N $,$ B $ 两点在折线数轴上的和谐距离相等？(请写出解题过程)

当点 $M$ 在 $OA$ 上，即 $t$ 在 0 和 2 之间(不含 0)时，点 $M$ 表示的数为 $4t - 8$，点 $N$ 表示的数为 $18 - 3t$，依题意得 $0-(4t - 8)=(18 - 3t)-6$，解得 $t=-4$ (不合题意，舍去)；当点 $M$ 在折线段 $O - B - C$ 上，即 $t$ 在 2 和 8 之间(不含 2)时，点 $M$ 表示的数为 $2t - 4$，点 $N$ 表示的数为 $18 - 3t$，依题意得 $2t - 4=(18 - 3t)-6$，或 $2t - 4 = 6-(18 - 3t)$，解得 $t=\frac{16}{5}$ 或 $t = 8$；当点 $M$ 在 $CD$ 上，即 $t$ 在 8 和 $\frac{26}{3}$ 之间(不含 8)时，点 $M$ 表示的数为 $4(t - 8)+12$，点 $N$ 表示的数为 $18 - 3t$，则点 $N$ 在点 $B$ 的左侧，依题意得 $4(t - 8)+12 = 6-(18 - 3t)$，解得 $t = 8$ (不合题意，舍去)。综上，当 $t$ 为 $\frac{16}{5}s$ 或 $8s$ 时，$M$，$O$ 两点在折线数轴上的和谐距离与 $N$，$B$ 两点在折线数轴上的和谐距离相等。

答案：(1) 12
(2) $\frac{22}{5}$ 解析:当点 $M$ 运动到点 $O$ 时，$t=\frac{8}{4}=2(s)$，当点 $M$ 运动到点 $C$ 时，$t=\frac{8}{4}+\frac{12}{2}=8(s)$，当点 $N$ 运动到点 $C$ 时，$t=\frac{18 - 12}{3}=2(s)$，当点 $N$ 运动到点 $O$ 时，$t=\frac{18}{3}=6(s)$，所以当点 $M$，$N$ 都运动到折线段 $O - B - C$ 上时，$t$ 在 2 和 6 之间，所以点 $M$ 表示的数为 $2(t - 2)=2t - 4$，点 $N$ 表示的数为 $18 - 3t$，所以 $O$，$M$ 两点间的和谐距离 $|OM|=2t - 4$；$C$，$N$ 两点间的和谐距离 $|CN|=|18 - 3t - 12|=3t - 6$；当 $M$，$N$ 两点相遇时，$2t - 4 + 3t - 6 = 12$，解得 $t=\frac{22}{5}$。
(3) $\frac{18}{5}$ 或 $\frac{26}{5}$ 解析:由(2)可得当 $M$，$N$ 两点相遇前相距 4 个单位长度，则 $2t - 4 + 3t - 6 + 4 = 12$，解得 $t=\frac{18}{5}$，相遇后相距 4 个单位长度，则 $2t - 4 + 3t - 6 - 4 = 12$，解得 $t=\frac{26}{5}$。
(4) 当点 $M$ 在 $OA$ 上，即 $t$ 在 0 和 2 之间(不含 0)时，点 $M$ 表示的数为 $4t - 8$，点 $N$ 表示的数为 $18 - 3t$，依题意得 $0-(4t - 8)=(18 - 3t)-6$，解得 $t=-4$ (不合题意，舍去)；当点 $M$ 在折线段 $O - B - C$ 上，即 $t$ 在 2 和 8 之间(不含 2)时，点 $M$ 表示的数为 $2t - 4$，点 $N$ 表示的数为 $18 - 3t$，题意得 $2t - 4=(18 - 3t)-6$，或 $2t - 4 = 6-(18 - 3t)$，解得 $t=\frac{16}{5}$ 或 $t = 8$；当点 $M$ 在 $CD$ 上，即 $t$ 在 8 和 $\frac{26}{3}$ 之间(不含 8)时，点 $M$ 表示的数为 $4(t - 8)+12$，点 $N$ 表示的数为 $18 - 3t$，则点 $N$ 在点 $B$ 的左侧，依题意得 $4(t - 8)+12 = 6-(18 - 3t)$，解得 $t = 8$ (不合题意，舍去)。综上，当 $t$ 为 $\frac{16}{5}s$ 或 8s 时，$M$，$O$ 两点在折线数轴上的和谐距离与 $N$，$B$ 两点在折线数轴上的和谐距离相等。