5. (2025·南京期中)某商户去批发市场购买了单价为 $ m $ 元的甲糖果 $ 20 $ 斤和单价为 $ n $ 元的乙糖果 $ 10 $ 斤,然后将两种糖果混合,以单价 $ \frac { m + n } { 2 } $ 元全部卖出,若 $ m > n $,则关于该商户的盈亏情况,判断正确的是(
A
)
A.赔了
B.赚了
C.不赔不赚
D.无法确定
答案:A 解析:$(20 + 10)\frac{m + n}{2}-20m - 10n = 15m + 15n - 20m - 10n = 5n - 5m = 5(n - m)$,因为 $m > n$,所以 $5(n - m)<0$,所以该商户赔了。故选 A。
6. (2024·无锡期中)某野生动物园门票价格为 $ 60 $ 元/张,并推出了两种购票方案,且两种方案不能同时使用。
|方案一:当团购门票数不超过 $ 40 $ 张时,无优惠;当团购门票数超过 $ 40 $ 张时,超过的部分每张优惠 $ 10 $ 元。|方案二:爱心捐款认养小动物,每捐款 $ 500 $ 元,则所购门票每张优惠 $ 2 $ 元;且捐款额必须为 $ 500 $ 的整数倍,最多捐款 $ 5000 $ 元。|
设某旅游团一次性购买门票 $ x $ 张($ x $ 为正整数)。
(1)如果选择方案一,求该旅游团购买门票的费用。
当0<x≤40时,费用为60x元;当x>40时,费用为(50x + 400)元。
(2)如果选择方案二,该旅游团爱心捐款 $ m $ 个 $ 500 $ 元($ m $ 为正整数)。
① 该旅游团一共需要花费的总费用为______元;(用含 $ m $,$ x $ 的代数式表示)
60x + 500m - 2mx
② 当 $ x > 40 $ 时,无论 $ x $ 取什么值,都存在一个正整数 $ m $,使选择方案二的总费用始终比选择方案一的总费用多某个固定值,则 $ m $ 的值为______,固定值为______。
5
2100
答案:(1) 由题意可得,如果选择方案一,当$0 < x \leq 40$时,总费用可表示为$60x$元;当$x > 40$时,总费用可表示为$60×40+(x - 40)×(60 - 10)=(50x + 400)$元。
(2)① $(60x + 500m - 2mx)$ 解析: 总费用可表示为 $500m+(60 - 2m)x = (60x + 500m - 2mx)$ 元。
② 5 2100 解析:$(60x + 500m - 2mx)-(50x + 400)=60x + 500m - 2mx - 50x - 400=(10 - 2m)x+(500m - 400)$,因为当 $x>40$ 时,无论 $x$ 取什么值,都存在一个正整数 $m$,使选择方案二的总费用始终比选择方案一的总费用多某个固定值,所以 $10 - 2m = 0$,得 $m = 5$,则 $500m - 400 = 500×5 - 400 = 2100$。即 $m$ 的值是 5,此固定值是 2100。
7. (2024·常州期中)工厂接到订单,需要边长为 $ ( a + 3 ) $ 和 $ 3 $ 的两种正方形卡纸。
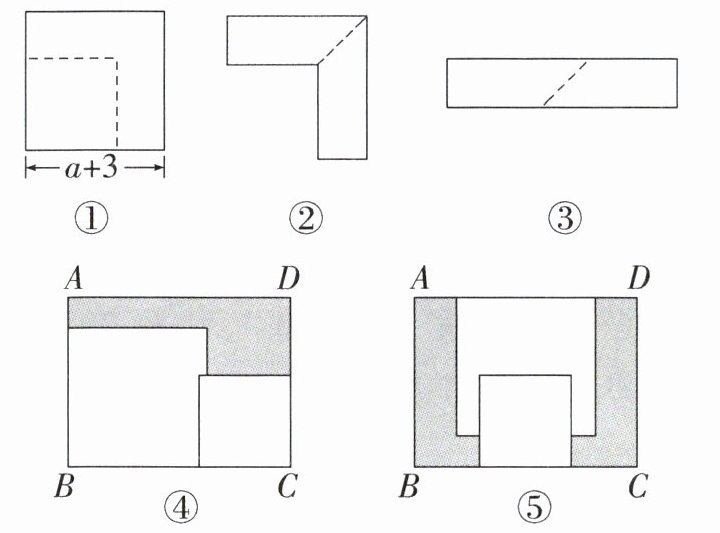
(1)仓库只有边长为 $ ( a + 3 ) $ 的正方形卡纸,现决定将部分边长为 $ ( a + 3 ) $ 的正方形卡纸,按图①所示裁剪得边长为 $ 3 $ 的正方形卡纸。
① 如图②,当 $ a = 2 $ 时,裁剪正方形后剩余部分的面积为______
16
;
② 剩余部分沿虚线又剪拼成一个如图③所示的长方形(不重叠无缝隙),则拼成的长方形的周长为______
4a + 12
。(用含 $ a $ 的代数式表示)
(2)若将裁得的正方形卡纸与原有正方形卡纸放入长方体盒子底部,按图④,图⑤两种方式放置(图④,图⑤中两张正方形卡纸均有部分重叠),盒子底部中未被这两张正方形卡纸覆盖的部分用阴影表示,设图④中阴影部分的面积为 $ S _ { 1 } $,图⑤中阴影部分的面积为 $ S _ { 2 } $,测得盒子底部长方形长比宽多 $ 5 $,则 $ S _ { 2 } - S _ { 1 } $ 的值为______
15
。
答案:(1)① 16 解析:因为 $a = 2$,根据题意,得 $(2 + 3)^{2}-3^{2}=25 - 9 = 16$。
② $4a + 12$ 解析:拼成的长方形的宽是 $a + 3 - 3 = a$,长为 $a + 3 + 3 = a + 6$,所以拼成的长方形的周长为 $2(a + a + 6)=4a + 12$。
(2) 15 解析:因为盒子底部长方形长比宽多 5,设盒子底部长方形的宽 $AB = x$,则长 $BC = x + 5$,则 $S_{1}=x(x + 5)-(a + 3)^{2}-3^{2}+3(a + 3 + 3 - x - 5)$,$S_{2}=x(x + 5)-(a + 3)^{2}-3^{2}+3(a + 3 + 3 - x)$,所以 $S_{2}-S_{1}=15$。
8. 我们知道绝对值的几何意义为数轴上一点到原点的距离。如 $ | 5 | $ 的几何意义为表示 $ 5 $ 的点到原点的距离,也可理解为 $ | 5 | = | 5 - 0 | $,即表示 $ 5 $ 的点到表示 $ 0 $ 的点的距离。又如 $ | 5 - 3 | $ 表示 $ 5 $,$ 3 $ 在数轴上对应的两点之间的距离,一般地,点 $ A $,$ B $ 在数轴上分别表示有理数 $ a $,$ b $,那么 $ A $,$ B $ 之间的距离可表示为 $ | a - b | $。
(1)$ | x - 1 | + | x - 2 | + | x - 3 | + | x - 4 | + … + | x - 50 | $ 的最小值是______
625
;
(2)求 $ | a + 3 | + 2 | a - 2 | + 3 | a - 4 | $ 的最小值
11
;
(3)$ ( | x + 1 | + | x - 2 | ) ( | y - 2 | + | y + 1 | ) ( | z - 3 | + | z + 1 | ) = 36 $,求 $ x + 2 y + 3 z $ 的最大值和最小值
最大值为15,最小值为-6
。
答案:(1) 625 解析:根据绝对值的几何意义与奇点偶段法可知,当 $x$ 在 $25\cdots26$ 之间时(含端点)有最小值为 $|x - 1|+|x - 2|+|x - 3|+|x - 4|+\cdots+|x - 50|=x - 1 + x - 2 + x - 3 + x - 4+\cdots+x - 25 + 26 - x + 27 - x+\cdots+50 - x=-1 - 2 - 3 - 4-\cdots-25 + 26 + 27+\cdots+49 + 50 = 625$。
(2) 11 解析:解法一:$|a + 3|+|a - 2|+|a - 2|+|a - 4|+|a - 4|+|a - 4|$ 的几何意义为表示 $a$ 的点分别到点 $-3$,$2$,$2$,$4$,$4$,$4$ 的距离之和,当 $a$ 在 $2\sim4$ 间时(含端点)有最小值,此时原式 $=11$。
解法二:当 $a$ 大于等于 4 时,$|a + 3|+2|a - 2|+3|a - 4|=a + 3 + 2a - 4 + 3a - 12 = 6a - 13$,当 $a = 4$ 时,取得最小值为 $6×4 - 13 = 11$;当 $a$ 在 2 和 4 之间(不含 4)时,$|a + 3|+2|a - 2|+3|a - 4|=a + 3 + 2a - 4 - 3a + 12 = 11$;当 $a$ 在 $-3$ 和 2 之间(不含 2)时,$|a + 3|+2|a - 2|+3|a - 4|=a + 3 - 2a + 4 - 3a + 12 = -4a + 19$,此时无最小值;当 $a<-3$ 时,$|a + 3|+2|a - 2|+3|a - 4|=-a - 3 - 2a + 4 - 3a + 12 = -6a + 13$,此时无最小值。综上可得,式子的最小值为 11。
(3) $|x + 1|+|x - 2|$ 表示数轴上表示数 $x$ 的点到表示 $-1$ 和 2 的点的距离之和,当 $x$ 在 $-1$ 与 2 之间时(含端点),$|x + 1|+|x - 2|=3$,当 $x$ 在 $-1$ 的左侧时,$x$ 到 2 的距离大于 3,当 $x$ 在 2 的右侧时,$x$ 到 $-1$ 的距离大于 3,所以当 $x$ 在 $-1$ 和 2 之间时,$|x + 1|+|x - 2|$ 有最小值 3,同理,当 $y$ 在 $-1$ 和 2 之间时,$|y - 2|+|y + 1|$ 有最小值 3,当 $z$ 在 $-1$ 和 3 之间时,$|z - 3|+|z + 1|$ 有最小值 4。
因为 $(|x + 1|+|x - 2|)(|y - 2|+|y + 1|)(|z - 3|+|z + 1|)=36$,所以各自均取最小值,当 $x = -1$,$y = -1$,$z = -1$ 时,$x + 2y + 3z$ 的值最小,$x + 2y + 3z=-6$,当 $x = 2$,$y = 2$,$z = 3$ 时,$x + 2y + 3z$ 的值最大,$x + 2y + 3z = 15$。综上所述,$x + 2y + 3z$ 的最大值为 15,最小值为 $-6$。