14. (2025·武汉期中)已知:$[x]表示不超过x$的最大整数.例如:$[2.3] = 2$,$[-1.8] = -2$.令关于$k的等式f(k) = [\frac{k + 1}{4}] - [\frac{k}{4}]$($k$是整数).例如:$f(3) = [\frac{3 + 1}{4}] - [\frac{3}{4}] = 1$,则下列结论正确的有______.(填序号)
①②④
答案:14. ①②④ 解析:因为 $ f ( k ) = \left[ \frac { k + 1 } { 4 } \right] - \left[ \frac { k } { 4 } \right] $,所以 $ f ( 1 ) = \left[ \frac { 1 + 1 } { 4 } \right] - \left[ \frac { 1 } { 4 } \right] = 0 - 0 = 0 $,故①正确,符合题意;$ f ( k + 4 ) = \left[ \frac { k + 4 + 1 } { 4 } \right] - \left[ \frac { k + 4 } { 4 } \right] = \left[ 1 + \frac { k + 1 } { 4 } \right] - \left[ 1 + \frac { k } { 4 } \right] = \left[ \frac { k + 1 } { 4 } \right] - \left[ \frac { k } { 4 } \right] $,而 $ f ( k ) = \left[ \frac { k + 1 } { 4 } \right] - \left[ \frac { k } { 4 } \right] $,所以 $ f ( k + 4 ) = f ( k ) $,故②正确,符合题意;设 $ n $ 为正整数,当 $ k = 4 n $ 时,$ f ( k ) = \left[ \frac { 4 n + 1 } { 4 } \right] - \left[ \frac { 4 n } { 4 } \right] = n - n = 0 $,当 $ k = 4 n + 1 $ 时,$ f ( k ) = \left[ \frac { 4 n + 2 } { 4 } \right] - \left[ \frac { 4 n + 1 } { 4 } \right] = n - n = 0 $,当 $ k = 4 n + 2 $ 时,$ f ( k ) = \left[ \frac { 4 n + 3 } { 4 } \right] - \left[ \frac { 4 n + 2 } { 4 } \right] = n - n = 0 $,当 $ k = 4 n + 3 $ 时,$ f ( k ) = \left[ \frac { 4 n + 4 } { 4 } \right] - \left[ \frac { 4 n + 3 } { 4 } \right] = n + 1 - n = 1 $,所以 $ f ( k ) = 0 $ 或 1,故④正确,符合题意;由上可得,当 $ k = 4 n $,$ k = 4 n + 1 $ 时,$ f ( k ) = 0 $,$ f ( k + 1 ) = 0 $,此时 $ f ( k ) = f ( k + 1 ) $,当 $ k = 4 n + 2 $ 时,$ k + 1 = 4 n + 3 $,所以 $ f ( k ) = 0 $,$ f ( k + 1 ) = 1 $,所以此时 $ f ( k ) \lt f ( k + 1 ) $,当 $ k = 4 n + 3 $ 时,$ k + 1 = 4 n + 4 $,所以 $ f ( k ) = 1 $,$ f ( k + 1 ) = \left[ \frac { 4 n + 5 } { 4 } \right] - \left[ \frac { 4 n + 4 } { 4 } \right] = \left[ n + 1 + \frac { 1 } { 4 } \right] - [ n + 1 ] = 0 $,此时 $ f ( k ) \gt f ( k + 1 ) $,故③错误,不符合题意。故答案为①②④。
解析:
①②④
解析:
① $f(1)=\left[\frac{1+1}{4}\right]-\left[\frac{1}{4}\right]=[0.5]-[0.25]=0-0=0$,正确;
② $f(k+4)=\left[\frac{k+4+1}{4}\right]-\left[\frac{k+4}{4}\right]=\left[1+\frac{k+1}{4}\right]-\left[1+\frac{k}{4}\right]=\left[\frac{k+1}{4}\right]-\left[\frac{k}{4}\right]=f(k)$,正确;
③ 当 $k=4n+3$($n$为整数)时,$f(k)=1$,$f(k+1)=\left[\frac{4n+5}{4}\right]-\left[\frac{4n+4}{4}\right]=(n+1)-(n+1)=0$,此时 $f(k) > f(k+1)$,错误;
④ 设 $k=4n+m$($n$为整数,$m=0,1,2,3$):
$m=0$:$f(k)=\left[n+\frac{1}{4}\right]-[n]=n-n=0$;
$m=1$:$f(k)=\left[n+\frac{2}{4}\right]-[n+\frac{1}{4}]=n-n=0$;
$m=2$:$f(k)=\left[n+\frac{3}{4}\right]-[n+\frac{2}{4}]=n-n=0$;
$m=3$:$f(k)=\left[n+1\right]-[n+\frac{3}{4}]=n+1-n=1$;
综上,$f(k)=0$或$1$,正确。
故答案为①②④。
15. (12分)化简或求值:
(1)$-2(2a - 1) + 3(2 - a)$;
(2)$6x^{2} - 2[3x^{2}y - 3(-x^{2} + 2x^{2}y)]$;
(3)已知$2x + y = 3$,求代数式$3(x - 2y) + 5(x + 2y - 1) - 2$的值.
答案:(1) $ - 7 a + 8 $ (2) $ 6 x ^ { 2 } y $ (3) $ 3 ( x - 2 y ) + 5 ( x + 2 y - 1 ) - 2 = 3 x - 6 y + 5 x + 10 y - 5 - 2 = 8 x + 4 y - 7 $。因为 $ 2 x + y = 3 $,所以原式 $ = 4 ( 2 x + y ) - 7 = 4 × 3 - 7 = 5 $
解析:
(1) 解:$-2(2a - 1) + 3(2 - a)$
$=-4a + 2 + 6 - 3a$
$=-7a + 8$
(2) 解:$6x^{2} - 2[3x^{2}y - 3(-x^{2} + 2x^{2}y)]$
$=6x^{2} - 2[3x^{2}y + 3x^{2} - 6x^{2}y]$
$=6x^{2} - 2[-3x^{2}y + 3x^{2}]$
$=6x^{2} + 6x^{2}y - 6x^{2}$
$=6x^{2}y$
(3) 解:$3(x - 2y) + 5(x + 2y - 1) - 2$
$=3x - 6y + 5x + 10y - 5 - 2$
$=8x + 4y - 7$
因为$2x + y = 3$,所以原式$=4(2x + y) - 7 = 4×3 - 7 = 5$
16. (8分)先化简,再求值:若多项式$x^{2} - 2mx + 3与\frac{1}{3}nx^{2} + 2x - 1的差与x$的取值无关,求多项式$4mn - [3m - 2m^{2} - 6(\frac{1}{2}m - \frac{2}{3}mn + \frac{1}{6}n^{2})]$的值.
答案:$ 4 m n - \left[ 3 m - 2 m ^ { 2 } - 6 \left( \frac { 1 } { 2 } m - \frac { 2 } { 3 } m n + \frac { 1 } { 6 } n ^ { 2 } \right) \right] = 4 m n - 3 m + 2 m ^ { 2 } + 6 \left( \frac { 1 } { 2 } m - \frac { 2 } { 3 } m n + \frac { 1 } { 6 } n ^ { 2 } \right) = 4 m n - 3 m + 2 m ^ { 2 } + 3 m - 4 m n + n ^ { 2 } = 2 m ^ { 2 } + n ^ { 2 } $。因为多项式 $ x ^ { 2 } - 2 m x + 3 $ 与 $ \frac { 1 } { 3 } n x ^ { 2 } + 2 x - 1 $ 的差与 $ x $ 的取值无关,所以 $ x ^ { 2 } - 2 m x + 3 - \left( \frac { 1 } { 3 } n x ^ { 2 } + 2 x - 1 \right) = x ^ { 2 } - 2 m x + 3 - \frac { 1 } { 3 } n x ^ { 2 } - 2 x + 1 = \left( 1 - \frac { 1 } { 3 } n \right) x ^ { 2 } - ( 2 m + 2 ) x + 4 $,所以 $ 1 - \frac { 1 } { 3 } n = 0 $,$ 2 m + 2 = 0 $,解得 $ n = 3 $,$ m = - 1 $。当 $ n = 3 $,$ m = - 1 $ 时,原式 $ = 2 × ( - 1 ) ^ { 2 } + 3 ^ { 2 } = 2 + 9 = 11 $
解析:
解:先计算多项式的差:
$x^{2} - 2mx + 3 - \left(\frac{1}{3}nx^{2} + 2x - 1\right)$
$=x^{2} - 2mx + 3 - \frac{1}{3}nx^{2} - 2x + 1$
$=\left(1 - \frac{1}{3}n\right)x^{2} - (2m + 2)x + 4$
因为差与$x$的取值无关,所以含$x^2$和$x$的项系数为0:
$\begin{cases}1 - \frac{1}{3}n = 0 \\ 2m + 2 = 0\end{cases}$
解得:$n = 3$,$m = -1$
化简求值多项式:
$4mn - [3m - 2m^{2} - 6\left(\frac{1}{2}m - \frac{2}{3}mn + \frac{1}{6}n^{2}\right)]$
$=4mn - 3m + 2m^{2} + 6\left(\frac{1}{2}m - \frac{2}{3}mn + \frac{1}{6}n^{2}\right)$
$=4mn - 3m + 2m^{2} + 3m - 4mn + n^{2}$
$=2m^{2} + n^{2}$
将$m = -1$,$n = 3$代入:
原式$=2×(-1)^{2} + 3^{2} = 2 + 9 = 11$
答案:11
17. (9分)在城区老旧小区改造中,为了提高居民的宜居环境,某小区规划修建一个广场(如图).
(1)用含$m$,$n$的式子表示广场(阴影部分)的面积$S$;
(2)若$m = 30m$,$n = 20m$,修建每平方米需费用200元,用科学记数法表示修建广场的总费用$W$的值.
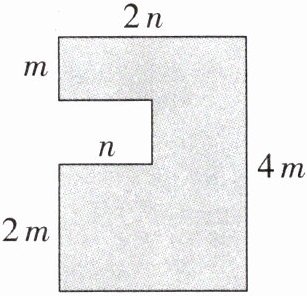
答案:(1) 由题意得 $ S = 4 m \cdot 2 n - ( 4 m - m - 2 m ) n = 7 m n $。(2) 当 $ m = 30 \mathrm { \ m } $,$ n = 20 \mathrm { \ m } $ 时,$ S = 7 m n = 7 × 30 × 20 = 4 200 ( \mathrm { m } ^ { 2 } ) $,因为每平方米需费用 200 元,所以修建广场的总费用 $ W = 4 200 × 200 = 840 000 $(元)$ = 8.4 × 10 ^ { 5 } $(元)
解析:
(1) 由题意得:
$S = 4m \cdot 2n - (4m - m - 2m)n = 8mn - mn = 7mn$
(2) 当 $m = 30\ \text{m}$,$n = 20\ \text{m}$ 时,
$S = 7mn = 7 × 30 × 20 = 4200\ \text{m}^2$
总费用 $W = 4200 × 200 = 840000 = 8.4 × 10^5$(元)