1. 下列各组代数式中是同类项的是(
C
)
A.5和3a
B.$2a^{2}b和-ab^{2}$
C.$3ab^{3}和-3b^{3}a$
D.$abc和a^{2}b^{2}c^{2}$
答案:C
解析:
解:同类项是指所含字母相同,并且相同字母的指数也相同的项。
A. 5是常数项,3a含有字母a,所含字母不同,不是同类项。
B. $2a^{2}b$中a的指数为2,b的指数为1;$-ab^{2}$中a的指数为1,b的指数为2,相同字母的指数不同,不是同类项。
C. $3ab^{3}$和$-3b^{3}a$所含字母都为a、b,且a的指数都为1,b的指数都为3,是同类项。
D. $abc$中各字母指数都为1,$a^{2}b^{2}c^{2}$中各字母指数都为2,相同字母的指数不同,不是同类项。
答案:C
2. 下列说法中,正确的是(
C
)
A.1不是单项式
B.$-\frac{xy}{5}$的系数是-5
C.$-x^{2}y$是三次单项式
D.$2x^{2}+3xy - 1$是四次三项式
答案:C
解析:
解:A.1是单项式,原说法错误;
B.$-\frac{xy}{5}$的系数是$-\frac{1}{5}$,原说法错误;
C.$-x^{2}y$是三次单项式,原说法正确;
D.$2x^{2}+3xy - 1$是二次三项式,原说法错误。
故选:C
3. 若$2025×14 = m$,则下列代数式表示$2025×15$的是(
D
)
A.$m + 1$
B.$2025m + 2025$
C.$m + 15$
D.$m + 2025$
答案:D
解析:
解:因为 $2025×14 = m$,所以 $2025×15 = 2025×(14 + 1) = 2025×14 + 2025×1 = m + 2025$。
D
4. 一种商品每件进价为$a$元,按进价增加20%定为售价,后因库存积压降价,按售价的八折出售,每件亏损(
D
)
A.$0.01a$元
B.$0.15a$元
C.$0.25a$元
D.$0.04a$元
答案:D
解析:
解:售价为:$a(1 + 20\%) = 1.2a$元
八折出售后的价格为:$1.2a × 80\% = 0.96a$元
亏损金额为:$a - 0.96a = 0.04a$元
答案:D
5. 定义一种新运算,规定:$a\oplus b = 3a - b$,若$a\oplus(-6b) = -2\frac{1}{4}$,请计算$(2a + b)\oplus(2a - 5b)$的值为(
B
)
A.-4
B.-3
C.3
D.4
答案:B
解析:
解:由新运算定义 $a\oplus b = 3a - b$,得
$a\oplus(-6b) = 3a - (-6b) = 3a + 6b$。
已知 $a\oplus(-6b) = -2\frac{1}{4} = -\frac{9}{4}$,
则 $3a + 6b = -\frac{9}{4}$,两边同除以3,得 $a + 2b = -\frac{3}{4}$。
计算 $(2a + b)\oplus(2a - 5b)$:
$\begin{aligned}(2a + b)\oplus(2a - 5b) &= 3(2a + b) - (2a - 5b) \\&= 6a + 3b - 2a + 5b \\&= 4a + 8b \\&= 4(a + 2b)\end{aligned}$
将 $a + 2b = -\frac{3}{4}$ 代入,得 $4×(-\frac{3}{4}) = -3$。
答案:B
6. (2025·重庆校级月考)对两个整式$M = x + y$,$N = x - y$,进行如下操作:记$P_{1} = M + N$,称为第一次操作;记$P_{2} = P_{1} + 2N$,称为第二次操作;记$P_{3} = P_{2} + 3M$,称为第三次操作;记$P_{4} = P_{3} + 4N$,称为第四次操作;…,下列说法:
①$P_{3} = 7$;
②若$x = y$,则$P_{2024} = P_{2025}$;
③若$x = -y = 1$,则不存在正整数$n$,使得$P_{n}$是10的倍数.
其中正确的个数是( )
B
A.0
B.1
C.2
D.3
答案:B 解析:已知 $ P _ { 1 } = M + N $,将 $ M = x + y $,$ N = x - y $ 代入可得 $ P _ { 1 } = ( x + y ) + ( x - y ) = 2 x $;已知 $ P _ { 2 } = P _ { 1 } + 2 N $,将 $ P _ { 1 } = 2 x $,$ N = x - y $ 代入可得 $ P _ { 2 } = 2 x + 2 ( x - y ) = 2 x + 2 x - 2 y = 4 x - 2 y $;已知 $ P _ { 3 } = P _ { 2 } + 3 M $,将 $ P _ { 2 } = 4 x - 2 y $,$ M = x + y $ 代入可得 $ P _ { 3 } = ( 4 x - 2 y ) + 3 ( x + y ) = 4 x - 2 y + 3 x + 3 y = 7 x + y $;已知 $ P _ { 4 } = P _ { 3 } + 4 N $,将 $ P _ { 3 } = 7 x + y $,$ N = x - y $ 代入可得 $ P _ { 4 } = ( 7 x + y ) + 4 ( x - y ) = 7 x + y + 4 x - 4 y = 11 x - 3 y $。①由上述计算可知 $ P _ { 3 } = 7 x + y $,题干未说明 $ x $,$ y $ 的取值,所以 $ P _ { 3 } $ 不一定等于 7,故说法①错误;②当 $ x = y $ 时,$ N = x - y = 0 $,$ M = x + y = 2 x $,所以 $ P _ { 2 } = P _ { 1 } + 2 N = P _ { 1 } $,$ P _ { 4 } = P _ { 3 } + 4 N = P _ { 3 } $,$ P _ { 6 } = P _ { 5 } + 6 N = P _ { 5 } $,$\cdots$,$ P _ { 2022 } = P _ { 2024 } = 2 025 × 2 x $,故说法②错误;③当 $ x = - 1 $ 时,即 $ x = - 1 $,$ y = 0 $,此时 $ M = x + y = - 1 + 0 = - 1 $,$ N = x - y = - 1 - 0 = - 1 $,$ P _ { 1 } = M + N = - 1 + ( - 1 ) = - 2 $,$ P _ { 2 } = P _ { 1 } + 2 N = - 2 + 2 × ( - 1 ) = - 2 - 2 = - 4 $,$ P _ { 3 } = P _ { 2 } + 3 M = - 4 + 3 × ( - 1 ) = - 4 - 3 = - 7 $,$ P _ { 4 } = P _ { 3 } + 4 N = - 7 + 4 × ( - 1 ) = - 7 - 4 = - 11 $,$ P _ { 5 } = P _ { 4 } + 5 M = - 11 + 5 × ( - 1 ) = - 11 - 5 = - 16 $,$ P _ { 6 } = P _ { 5 } + 6 N = - 16 + 6 × ( - 1 ) = - 16 - 6 = - 22 $,$\cdots$,发现所有 $ P _ { n } $ 的末位数字均为 2,4,6,不会出现 0,则不存在正整数 $ n $,使得 $ P _ { n } $ 是 10 的倍数,故说法③正确。综上,正确的说法只有 1 个。故选 B。
7. 单项式$-\frac{\pi x^{3}y}{3}$的系数是
$ - \frac { \pi } { 3 } $
,多项式$2ab - 3a^{2}b^{2} + 1$的次数是
4
.
答案:$ - \frac { \pi } { 3 } $ 4
8. (2024·甘孜州中考)已知$x^{2} + 2x = 3$,那么$2x^{2} + 4x - 5$的值是
1
.
答案:1
解析:
解:因为$x^{2} + 2x = 3$,所以$2(x^{2} + 2x) = 2×3$,即$2x^{2} + 4x = 6$。
则$2x^{2} + 4x - 5 = 6 - 5 = 1$。
1
9. (青海中考)已知单项式$2a^{4}b^{-2m + 7}与3a^{2m}b^{n + 2}$是同类项,则$m + n = $
3
.
答案:3
解析:
解:因为单项式$2a^{4}b^{-2m + 7}$与$3a^{2m}b^{n + 2}$是同类项,所以同类项对应字母的指数相等。
对于字母$a$:$4 = 2m$,解得$m = 2$。
对于字母$b$:$-2m + 7 = n + 2$,将$m = 2$代入得:$-2×2 + 7 = n + 2$,即$3 = n + 2$,解得$n = 1$。
所以$m + n = 2 + 1 = 3$。
3
10. (连云港中考)按照如图所示的计算程序,若$x = 2$,则输出的结果是
-26
.
答案:- 26
解析:
当$x = 2$时,计算$10 - x^2 = 10 - 2^2 = 10 - 4 = 6$。因为$6 \geq 0$,所以将$6$作为新的$x$代入计算。
此时$x = 6$,计算$10 - x^2 = 10 - 6^2 = 10 - 36 = -26$。因为$-26 < 0$,所以输出结果为$-26$。
$-26$
11. 如图是一张长为$a$,宽为$b$的长方形纸片,小明在长方形纸片的四个角各剪去一个边长为$x$的小正方形,用代数式表示纸片剩余部分的周长为
$ 2 a + 2 b $
.
答案:$ 2 a + 2 b $
解析:
解:在长方形纸片的四个角各剪去一个边长为$x$的小正方形后,通过平移可知,剩余部分的周长与原长方形的周长相等。
原长方形的周长为$2(a + b) = 2a + 2b$。
故纸片剩余部分的周长为$2a + 2b$。
答案:$2a + 2b$
12. 如果$a和-4b$互为相反数,那么多项式$2(-b - 2a + 10) + 3(a + 2b - 3)$的值是
11
.
答案:11
解析:
解:因为$a$和$-4b$互为相反数,所以$a + (-4b) = 0$,即$a - 4b = 0$,$a = 4b$。
$\begin{aligned}&2(-b - 2a + 10) + 3(a + 2b - 3)\\=& -2b - 4a + 20 + 3a + 6b - 9\\=& (-4a + 3a) + (-2b + 6b) + (20 - 9)\\=& -a + 4b + 11\end{aligned}$
将$a = 4b$代入上式,得$-4b + 4b + 11 = 11$。
11
13. (2023·十堰中考改编)用火柴棍拼成如下图案,其中如图①,第1个图案由4个小等边三角形围成1个小四边形,如图②,第2个图案由6个小等边三角形围成2个小四边形,…,若按此规律拼下去,则第$n$个图案需要火柴棍的根数为______.(用含$n$的式子表示)
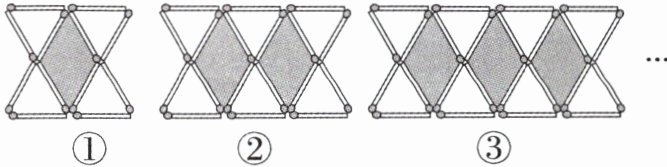
6n + 6
答案:13. $ 6 n + 6 $ 解析:当 $ n = 1 $ 时,有 $ 2 × ( 1 + 1 ) = 4 $(个)三角形;当 $ n = 2 $ 时,有 $ 2 × ( 2 + 1 ) = 6 $(个)三角形;当 $ n = 3 $ 时,有 $ 2 × ( 3 + 1 ) = 8 $(个)三角形;第 $ n $ 个图案有 $ 2 ( n + 1 ) = ( 2 n + 2 ) $ 个三角形,每个三角形需要三根火柴棍,故第 $ n $ 个图案需要火柴棍的根数为 $ 6 n + 6 $。
解析:
当$n=1$时,三角形个数为$2×(1+1)=4$;当$n=2$时,三角形个数为$2×(2+1)=6$;当$n=3$时,三角形个数为$2×(3+1)=8$;则第$n$个图案三角形个数为$2(n+1)=2n+2$。每个三角形需$3$根火柴棍,所以火柴棍根数为$3×(2n+2)=6n+6$。
$6n + 6$