现将 10 个数字按图所示排成一个圈,并设置了一种数字信息的加密规则:加密钥匙为“$n\And 5$”它代表把明文$n$换成图中从它开始顺时针跳过 5 个数字的那个数字.例如明文是 3,对应的密文是 9.若收到的密文是 2024,那么通过解密,它对应的明文是.

 2. (2025·盐城期中)【阅读材料】
在生活中,密码的应用随处可见,如电子支付、电子门禁、密码认证等.如今,密码学已成为网络信息安全的核心,密码学的研究使用了越来越多的数学工具.
有一种密码的明文(真实文)按计算机键盘上的字母顺序排列,如$Q,W,E,…,N,M$,这 26 个字母依次对应$1,2,3,…,25,26$这 26 个自然数(见下表).设明文的任一字母所对应的自然数为$x$,通过某种规定的运算程序把$x转化为对应的自然数x'$,$x'$对应的字母为密文.
| $Q$ | $W$ | $E$ | $R$ | $T$ | $Y$ | $U$ | $I$ | $O$ | $P$ | $A$ | $S$ | $D$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| $F$ | $G$ | $H$ | $J$ | $K$ | $L$ | $Z$ | $X$ | $C$ | $V$ | $B$ | $N$ | $M$ |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
 运算程序为:

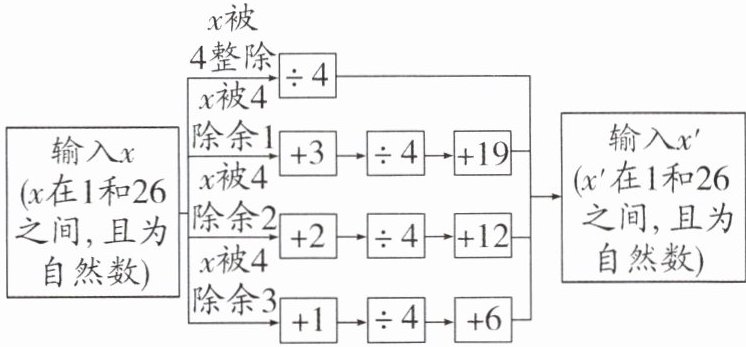
例如:将明文$M$转换成密文:$M\to 26$(26 被 4 除余 2)$\to \frac{26 + 2}{4}+12 = 19\to L$,即$M的密文为L$;将密文$P$转换成明文,$P\to 10\to (10 - 6)× 4-1 = 15\to G$,即$P的明文为G$.
 【解决问题】
(1)按照以上程序加密 1 次,明文$I$对应的密文为____;明文$NLZF$对应的密文为____.
(2)按照以上程序加密 1 次的密文为“康居学子”的首字母“$KJXZ$”,则其对应的明文为____.
(3)加密可以重复进行,按照以上程序加密 2024 次,求明文$V$对应的密文.
错题
视频讲题