2025年学霸题中题七年级数学上册苏科版第57页解析答案

12. 如图是一个运算程序的示意图,若开始输入的x的值为81,我们看到第一次输出的结果为27,第二次输出的结果为9……第2024次输出的结果为

答案：1 解析：第1次，$\frac{1}{3}×81 = 27$；第2次，$\frac{1}{3}×27 = 9$；第3次，$\frac{1}{3}×9 = 3$；第4次，$\frac{1}{3}×3 = 1$；第5次，$1 + 2 = 3$；第6次，$\frac{1}{3}×3 = 1$，…，以此类推，从第3次开始以3，1循环，因为$(2024 - 2)÷2 = 1011$，所以第2024次输出的结果为1。

13. (2025·济南期末)如图①是1个直角三角形和2个正方形,直角三角形的三条边长分别是a,b,c,其中a,b是直角边.正方形的边长分别是a,b.

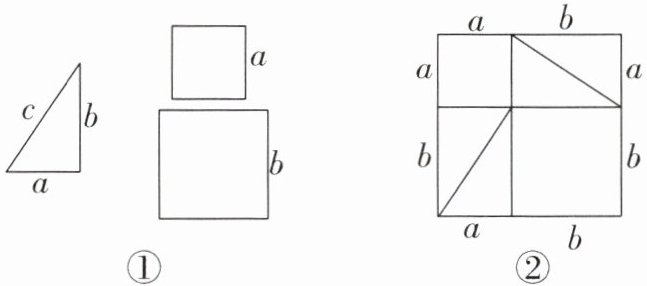
(1)将4个完全一样的直角三角形和2个正方形组成一个大正方形(如图②).用两种不同的方法列代数式表示图②中的大正方形的面积:
方法一:

$a^{2} + 2ab + b^{2}$

;方法二:

$(a + b)^{2}$

.
(2)观察图②,试写出$(a+b)^{2},a^{2},2ab,b^{2}$这四个代数式之间的等量关系:

$a^{2} + 2ab + b^{2} = (a + b)^{2}$

.
(3)请利用(2)中的等量关系解决问题:已知图①中三角形的面积是6,图②中大正方形的面积是49,求$a^{2}+b^{2}$的值.

由于题图①中三角形的面积是6，所以$ab = 12$。因为$a^{2} + 2ab + b^{2} = (a + b)^{2}$，所以$a^{2} + b^{2} = (a + b)^{2} - 2ab = 49 - 2×12 = 25$。

(4)求$3.14^{2}+6.28×6.86+6.86^{2}$的值.

$3.14^{2} + 6.28×6.86 + 6.86^{2} = 3.14^{2} + 2×3.14×6.86 + 6.86^{2} = (3.14 + 6.86)^{2} = 10^{2} = 100$。

答案：(1)$a^{2} + 2ab + b^{2}$ $(a + b)^{2}$(2)$a^{2} + 2ab + b^{2} = (a + b)^{2}$(3)由于题图①中三角形的面积是6，所以$ab = 12$。因为$a^{2} + 2ab + b^{2} = (a + b)^{2}$，所以$a^{2} + b^{2} = (a + b)^{2} - 2ab = 49 - 2×12 = 25$。(4)$3.14^{2} + 6.28×6.86 + 6.86^{2} = 3.14^{2} + 2×3.14×6.86 + 6.86^{2} = (3.14 + 6.86)^{2} = 10^{2} = 100$。

解析：

(1)方法一：$(a+b)^{2}$；方法二：$a^{2}+2ab+b^{2}$
(2)$(a+b)^{2}=a^{2}+2ab+b^{2}$
(3)解：因为图①中三角形的面积是6，所以$\frac{1}{2}ab=6$，即$ab=12$。
因为图②中大正方形的面积是49，所以$(a+b)^{2}=49$。
由(2)知$a^{2}+b^{2}=(a+b)^{2}-2ab$，所以$a^{2}+b^{2}=49-2×12=25$。
(4)解：$3.14^{2}+6.28×6.86+6.86^{2}=3.14^{2}+2×3.14×6.86+6.86^{2}=(3.14+6.86)^{2}=10^{2}=100$。

14. 已知$(-2x+1)^{5}= a_{5}x^{5}+a_{4}x^{4}+a_{3}x^{3}+a_{2}x^{2}+a_{1}x+a_{0}$是关于x的恒等式(即x取任意值时等式都成立),则$a_{1}+a_{2}+a_{3}+a_{4}+a_{5}= $

-2

答案：−2 解析：当$x = 0$时，$a_{0} = 1$；当$x = 1$时，$a_{5} + a_{4} + a_{3} + a_{2} + a_{1} + a_{0} = -1$，则$a_{1} + a_{2} + a_{3} + a_{4} + a_{5} = -2$。

解析：

解：当$x = 0$时，$(-2×0 + 1)^5 = a_5×0^5 + a_4×0^4 + a_3×0^3 + a_2×0^2 + a_1×0 + a_0$，即$a_0 = 1$；
当$x = 1$时，$(-2×1 + 1)^5 = a_5×1^5 + a_4×1^4 + a_3×1^3 + a_2×1^2 + a_1×1 + a_0$，即$a_5 + a_4 + a_3 + a_2 + a_1 + a_0 = (-1)^5 = -1$；
所以$a_1 + a_2 + a_3 + a_4 + a_5 = -1 - a_0 = -1 - 1 = -2$。
$-2$

15. 在学习代数式的值时,介绍了计算程序:用“$□$”表示数据输入、输出框;用“$□$”表示数据处理和运算框;用“$\lozenge$”表示数据判断框(根据条件决定执行两条路径中的某一条).
(1)①如图①,当输入$x= -2$时,输出$y= $____;
②如图②,第一个运算框“$□$”内应填____;第二个运算框“$□$”内应填____.
(2)①如图③,当输入$x= -1$时,输出$y= $____;
②如图④,当输出$y= 37$时,输入的值$x= $____.
(3)为鼓励节约用水,政府决定对用水实行“阶梯价”:
当每月用水量不超过15t(含15t)时,以2元/t的价格收费;当每月用水量超过15t时,超过部分以3元/t的价格收费.请设计出一个“计算程序”,使得输入数为每月用水量x,输出数为水费y.

答案：
(1)①−9 ②×5 −3 (2)①−43 ②42或−6 解析：①当$x = -1$时，$y = -1×2 - 5 = -7 ＞ -20$，$-7×2 - 5 = -19 ＞ -20$，$-19×2 - 5 = -43 ＜ -20$，故答案为-43。②分为两种情况：当$x ＞ 0$时，$x - 5 = 37$，解得$x = 42$；当$x ＜ 0$或$x = 0$时，$x^{2} + 1 = 37$，解得$x = -6$(舍去正数)。故答案为42或-6。(3)因为当每月用水量不超过15t(含15t)时，以2元/t的价格收费；当每月用水量超过15t时，超过部分以3元/t 的价格收费，所以水费收费分两种情况：$x ≤ 15$和$x ＞ 15$，分别计算。所以可以设计计算程序如图所示