9. 若$ x $表示一个两位数,$ y $也表示一个两位数,小明想用$ x $,$ y $来组成一个四位数,且把$ x $放在$ y $的右边,则这个四位数表示为
$100y + x$
.
答案:$100y + x$
解析:
解:因为$x$是两位数,$y$是两位数,把$x$放在$y$的右边,相当于$y$扩大了$100$倍,$x$的位置不变,所以这个四位数表示为$100y + x$。
$100y + x$
10. 新考法(2024·雅安中考)如图是1
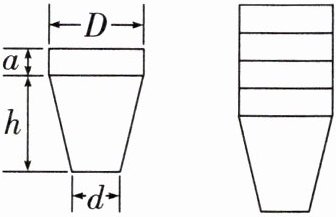
个纸杯和若干个叠放在一起的纸杯的示意图,在探究纸杯叠放在一起后的总高度$ H 与杯子数量 n $的变化规律的活动中,我们可以获得以下数据(字母),请选用适当的字母表示$ H = $
$h + an$
.
①杯子底部到杯沿底边的高$ h $; ②杯口直径$ D $; ③杯底直径$ d $; ④杯沿高$ a $.
答案:$h + an$
11. 泰兴某企业有$ m \mathrm { t } $煤,计划用$ n $天,为积极响应市政府“节能减排”的号召,现打算多用5天,则现在比原计划每天少用煤
$(\frac {m}{n}-\frac {m}{n + 5})$
$\mathrm { t } $.
答案:$(\frac {m}{n}-\frac {m}{n + 5})$
解析:
原计划每天用煤量为$\frac{m}{n}$ t,现在计划用$(n + 5)$天,现在每天用煤量为$\frac{m}{n + 5}$ t,现在比原计划每天少用煤$(\frac{m}{n}-\frac{m}{n + 5})$ t。
$(\frac{m}{n}-\frac{m}{n + 5})$
12. 某人去水果批发市场采购苹果,他看中了A,B两家苹果.这两家苹果品质一样,零售价都为6元/kg,批发价各不相同.
A家规定:批发质量不超过1000kg,价格按零售价的92%;批发质量超过1000kg但不超过2000kg,价格按零售价的90%;批发质量超过2000kg,价格按零售价的88%.
B家的规定如表:
|质量范围/kg|0~500|500~1500|1500~2500|2500以上|
|价格/元|零售价的95%|零售价的85%|零售价的75%|零售价的70%|
表格说明:批发价格分段计算,如:某人批发苹果2100kg,则总费用$ = 6 × 95 \% × 500 + 6 × 85 \% × 1000 + 6 × 75 \% × ( 2100 - 1500 ) $.
(1)如果他批发600kg苹果,那么他在A家批发需要
3312
元,在B家批发需要
3360
元.
(2)如果他批发$ x \mathrm { kg } $苹果($ 1500 < x < 2000 $),那么他在A家批发需要
5.4x
元,在B家批发需要
(4.5x + 1200)
元.(用含$ x $的代数式表示)
(3)现在他要批发1800kg苹果,你能帮助他选择在哪家批发更优惠吗? 请说明理由.
选择 B 家更优惠.理由:在 A 家批发需要$90\%×6×1 800 = 9 720$(元),在 B 家批发需要$500×95\%×6 + 1 000×85\%×6 + 300×75\%×6 = 9 300$(元),$9 300 < 9 720$,所以选择 B 家批发更优惠.
答案:(1)3 312 3 360 解析:在 A 家批发需要$600×92\%×6 = 3 312$(元),在 B 家批发需要$500×95\%×6 + (600 - 500)×85\%×6 = 2 850 + 510 = 3 360$(元).(2)$5.4x$ $(4.5x + 1 200)$ 解析:如果他批发$x\ kg$苹果$(1 500 < x < 2 000)$,在 A 家批发需要$90\%x×6 = 5.4x$(元),在 B 家批发需要$500×95\%×6 + 1 000×85\%×6 + (x - 1 500)×75\%×6 = (4.5x + 1 200)$元.(3)选择 B 家更优惠.理由:在 A 家批发需要$90\%×6×1 800 = 9 720$(元),在 B 家批发需要$500×95\%×6 + 1 000×85\%×6 + 300×75\%×6 = 9 300$(元),$9 300 < 9 720$,所以选择 B 家批发更优惠.
解析:
(1)3312;3360
解:A家:$600×6×92\% = 600×6×0.92 = 3312$(元)
B家:$500×6×95\% + (600 - 500)×6×85\% = 500×6×0.95 + 100×6×0.85 = 2850 + 510 = 3360$(元)
(2)$5.4x$;$4.5x + 1200$
解:A家:$x×6×90\% = 5.4x$(元)
B家:$500×6×95\% + 1000×6×85\% + (x - 1500)×6×75\% = 2850 + 5100 + 4.5(x - 1500) = 7950 + 4.5x - 6750 = 4.5x + 1200$(元)
(3)选择B家更优惠。
解:A家:$1800×6×90\% = 1800×5.4 = 9720$(元)
B家:$500×6×95\% + 1000×6×85\% + (1800 - 1500)×6×75\% = 2850 + 5100 + 300×4.5 = 7950 + 1350 = 9300$(元)
∵$9300<9720$,∴选择B家更优惠。
13. 如图①是等边三角形,第一次操作,将一个等边三角形每边三等分,再以中间一段为边向外作等边三角形,然后去掉中间一段,得到边数为12的图②.第二次操作,将图②中的每条线段三等分,重复上面的操作,得到边数为48的图③.如此循环下去,得到一个周长无限的“雪花曲线”.操作$ n $次后所得“雪花曲线”的边数是
$3×4^{n}$(n 为正整数)
.
答案:$3×4^{n}$(n 为正整数) 解析:开始时,等边三角形的边数为 3,第 1 次操作后所得“雪花曲线”的边数为$12 = 3×4$,第 2 次操作后所得“雪花曲线”的边数为$48 = 12×4 = 3×4×4 = 3×4^{2}$,第 3 次操作后所得“雪花曲线”的边数为$3×4^{3} = 192$,归纳类推得第 n 次操作后所得“雪花曲线”的边数为$3×4^{n}$,其中 n 为正整数.
解析:
开始时,等边三角形的边数为3。
第1次操作后,边数为$12 = 3×4$;
第2次操作后,边数为$48 = 3×4×4 = 3×4^{2}$;
归纳可得,第n次操作后,边数为$3×4^{n}$(n为正整数)。
$3×4^{n}$
14. (2025·温州期末)如图是两个未完成的二阶幻圆的模型,要求内外两个圆上的四个数之和及外圆直径上的四个数之和都相等,则图①中$ m = $
0.2
;图②中$ n = $
$a + b - c$
(用含$ a $,$ b $,$ c $的代数式表示).

答案:0.2 $a + b - c$ 解析:由题图①可知,$-9 + 5 + 11 + 2 = -9 + 6.8 + m + 11$,得$m = 0.2$.由题图②知$-9 + a + 11 + b = -9 + c + n + 11$,则$n = a + b - c$.
解析:
解:图①:由题意得,外圆上四个数之和为$-9 + 5 + 11 + 2$,外圆直径上四个数之和为$-9 + 6.8 + m + 11$,因为两者相等,所以$-9 + 5 + 11 + 2 = -9 + 6.8 + m + 11$,解得$m = 0.2$。
图②:由题意得,外圆上四个数之和为$-9 + a + 11 + b$,外圆直径上四个数之和为$-9 + c + n + 11$,因为两者相等,所以$-9 + a + 11 + b = -9 + c + n + 11$,解得$n = a + b - c$。
0.2;$a + b - c$