1.(2024·常州期中)如果一个长方形的周长为12,其中长为a,那么该长方形的宽为(
B
)
A.$12 - a$
B.$6 - a$
C.$6a$
D.$8 - a$
答案:B
解析:
解:长方形周长=2×(长+宽),已知周长为12,长为a,设宽为b。
则12=2×(a+b),
等式两边同时除以2得:6=a+b,
移项得:b=6 - a。
答案:B
2.一个三位数的百位上是a,十位上是b,个位上是c,这个三位数可以表示为(
D
)
A.$a + b + c$
B.$abc$
C.$100c + 10b + a$
D.$100a + 10b + c$
答案:D
解析:
解:一个三位数,百位上是$a$,表示$a$个$100$,即$100a$;十位上是$b$,表示$b$个$10$,即$10b$;个位上是$c$,表示$c$个$1$,即$c$。所以这个三位数可以表示为$100a + 10b + c$。
D
3.(2025·抚顺期中)某校利用午休时间开展了主题为“行万里路,读万卷书”的读书活动.现在需要购买甲、乙两种儿童文学书籍共100本供学生阅读,其中甲种书籍的单价为10元/本,乙种书籍的单价为15元/本,设购买甲种书籍a本,则购买乙种书籍的费用为(
C
)
A.$15a$元
B.$10(100 - a)$元
C.$15(100 - a)$元
D.$(100 - 15a)$元
答案:C
解析:
解:购买甲种书籍$a$本,共购买100本,
则购买乙种书籍$(100 - a)$本。
乙种书籍单价15元/本,
购买乙种书籍的费用为$15(100 - a)$元。
答案:C
4.(1)(长春中考)长春市净月潭国家森林公园门票的价格为成人票每张30元,儿童票每张15元.若购买m张成人票和n张儿童票,则共需花费
(30m + 15n)
元.
(2)有三个连续奇数,其中最小的一个数是a,那么最大的一个数是
a + 4
.
(3)正方形的边长为a,当边长增加b时,它的面积增加
$(a + b)^2 - a^2$
.(不必化简)
(4)甲每小时走a km,乙每小时走b km,两人同时同地出发反向行走,2h后他们之间的距离为
(2a + 2b)
km.
答案:$(1) (30m + 15n) (2) a + 4 (3) (a + b)^2 - a^2 (4) (2a + 2b)$
5.教材P76练习T1(2)变式 用字母表示下图中各阴影部分的面积.
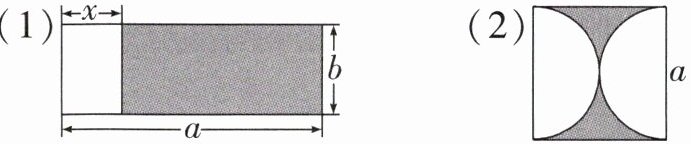
(3)

答案:(1) 阴影部分为长方形,长为 $(a - x)$,宽为 $b$,故面积为 $b(a - x)$。
(2) 阴影部分的面积等于正方形的面积减去 $2$ 个半圆的面积,故面积为 $a^2 - \pi\left(\frac{a}{2}\right)^2$。
(3) 阴影部分的面积一部分是半径为 $8$ 的四分之一圆,一部分是长为 $a$、宽为 $8$ 的长方形,还有一部分是直径为 $8$ 的半圆,故阴影部分的面积为 $\frac{1}{4}\pi×8^2 + 8a + \frac{1}{2}\pi×\left(\frac{8}{2}\right)^2 = 16\pi + 8a + 8\pi = 8a + 24\pi$。
6.教材P76习题T2变式 用字母表示下列运算或数量关系:
(1)某数与$\frac{1}{2}$的差; (2)某数的$\frac{1}{2}与\frac{1}{3}$的和;
(3)某数与1的差的平方大于0;
(4)一个数是另一个数与2的乘积.
答案:(1) 设这个数为 $x$,“某数与 $\frac{1}{2}$ 的差”可以表示为 $x - \frac{1}{2}$。
(2) 设这个数为 $x$,“某数的 $\frac{1}{2}$ 与 $\frac{1}{3}$ 的和”可以表示为 $\frac{1}{2}x + \frac{1}{3}$。
(3) 设这个数为 $x$,“某数与 $1$ 的差的平方大于 $0$”可以表示为 $(x - 1)^2 > 0$。
(4) 设这个数为 $a$,另一个数为 $b$,“一个数是另一个数与 $2$ 的乘积”可以表示为 $a = 2b$。
7.右图是一个窗户的示意图,其上部是由4个相同的扇形组成的半圆形,下部是由边长为a的4个完全相同的小正方形组成的正方形,则做这个窗户需要的材料总长为(
B
)
A.$15a$
B.$15a + \pi a$
C.$15a + \pi a^{2}$
D.$\pi a + 6a$
答案:B 解析:由题图可知,需要长度为 $a$ 的材料的长为 $15a$,半圆弧长为 $\frac{1}{2}\pi×2a = \pi a$,所以共需材料总长为 $15a + \pi a$,故选 B。