2025年学霸题中题七年级数学上册苏科版第51页解析答案

19.(9分)(2025·常州期中)作为城市高质量发展“大动脉”的常州地铁,近年来为城市发展和居民生活提供了高效便捷的公共交通服务.其中1号线是常州市第一条开工建设的地铁线路,于2019年9月21日开通运营,这条线路呈南北走向,北起新北区森林公园站,途经天宁区,南至武进区南夏墅站.下图为1号线串联的部分站点.据统计,2024年10月1日至7日,常州地铁1号线客流量达135.13万人次.
(1)若135.13万人次用科学记数法表示为$1.3513×10^{n}$人次,则$n=$

.
(2)某天,小红同学从环球港站开始乘坐地铁1号线,在地铁各站点做志愿者服务,到A站下车时,本次志愿者服务活动结束,约定向南夏墅站方向为正,当天的乘车记录如下(单位：站)：+5,-2,-6,+8,+3,-4,-9,+8.
①请通过计算说明A站是哪一站？
②若相邻两站之间的平均距离为1.2千米,求这次小红志愿服务期间乘坐地铁行进的路程是多少千米？

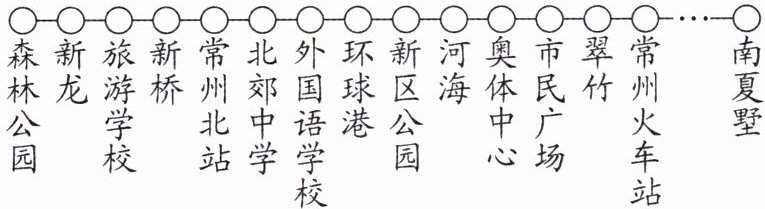
(2)①$(+5) + (-2) + (-6) + (+8) + (+3) + (-4) + (-9) + (+8) = 5 - 2 - 6 + 8 + 3 - 4 - 9 + 8 = 3$（站），所以由题意可知，A 站是奥体中心站。
②$(\vert + 5\vert + \vert - 2\vert + \vert - 6\vert + \vert + 8\vert + \vert + 3\vert + \vert - 4\vert + \vert - 9\vert + \vert + 8\vert)×1.2 = (5 + 2 + 6 + 8 + 3 + 4 + 9 + 8)×1.2 = 54$（千米），所以这次小红志愿服务期间乘坐地铁行驶进的路程是 54 千米。

答案：(1)6
(2)①$(+5) + (-2) + (-6) + (+8) + (+3) + (-4) + (-9) + (+8) = 5 - 2 - 6 + 8 + 3 - 4 - 9 + 8 = 3$（站），所以由题意可知，A 站是奥体中心站。
②$(\vert + 5\vert + \vert - 2\vert + \vert - 6\vert + \vert + 8\vert + \vert + 3\vert + \vert - 4\vert + \vert - 9\vert + \vert + 8\vert)×1.2 = (5 + 2 + 6 + 8 + 3 + 4 + 9 + 8)×1.2 = 54$（千米），所以这次小红志愿服务期间乘坐地铁行驶进的路程是 54 千米。

20.(9分)如图,将一根木棒放在数轴(单位长度为1cm)上,木棒左端与数轴上的点A重合,右端与数轴上的点B重合.

(1)若将木棒沿数轴向右水平移动,则当它的左端移动到点B时,它的右端在数轴上所对应的数为30；若将木棒沿数轴向左水平移动,则当它的右端移动到点A时,它的左端在数轴上所对应的数为3,由此可得这根木棒的长为______cm.
(2)图中点A所表示的数是______,点B所表示的数是______.
(3)受(1)(2)的启发,请借助“数轴”这个工具解决下列问题：一天,小明去问爷爷的年龄,爷爷说：“我若是你现在这么大,你还要37年才出生；你若是我现在这么大,我就119岁啦！”分别求爷爷和小明现在的年龄.

(1)

(2)

(3)

借助数轴(图略)，把小明和爷爷的年龄差看作木棒 AB，爷爷像小明这样大时，可看作点 B 向左移动到点 A，此时点 A 向左移后所对应的数为-37，所以爷爷比小明大[119 - (-37)]÷3 = 52（岁），所以爷爷现在的年龄为119 - 52 = 67（岁），所以小明现在的年龄为67 - 52 = 15（岁）。

答案：(1)9 解析:观察数轴可知三根这样的木棒长为$30 - 3 = 27$（cm），则这根木棒的长为$27÷3 = 9$（cm）。
(2)12 21 解析:由(1)可知这根木棒的长为 9 cm，所以点 A 表示的数为$3 + 9 = 12$，点 B 表示的数是$3 + 9 + 9 = 21$。
(3)借助数轴(图略)，把小明和爷爷的年龄差看作木棒 AB，爷爷像小明这样大时，可看作点 B 向左移动到点 A，此时点 A 向左移后所对应的数为$-37$，所以爷爷比小明大$[119 - (-37)]÷3 = 52$（岁），所以爷爷现在的年龄为$119 - 52 = 67$（岁），所以小明现在的年龄为$67 - 52 = 15$（岁）。

21.(10分)如图,数轴上有A,B,C三个点,A,B,C对应的数分别是a,b,10,满足$|a + 24|+|b + 10|= 0$,动点P从点A出发,以每秒1个单位的速度向终点C运动,设运动时间为t s.
(1)求a,b的值.
(2)写出点P表示的数(用含t的式子表示).
(3)若点P到点A的距离是点P到点B的距离的2倍,求点P对应的数.
(4)当点P运动到点B时,点Q从点A出发,以每秒3个单位的速度向点C运动,点Q到达点C后,再立即以同样的速度返回,当点Q在返回过程中与点P相遇时,两点停止运动.直接写出在点Q开始运动后第几秒时,P,Q两点之间的距离为4.
视频讲题

答案：(1)因为$\vert a + 24\vert + \vert b + 10\vert = 0$，所以$a + 24 = 0$，$b + 10 = 0$，所以$a = -24$，$b = -10$。
(2)由题意得，点 P 表示的数是$-24 + t$。
(3)因为点 P 到点 A 的距离是点 P 到点 B 的距离的 2 倍，所以$\vert -24 + t - (-24)\vert = 2\vert -24 + t - (-10)\vert$，即$\vert t\vert = 2\vert t - 14\vert$，解得$t = 28$或$t = \frac{28}{3}$，当$t = 28$时，$-24 + t = -24 + 28 = 4$；当$t = \frac{28}{3}$时，$-24 + t = -24 + \frac{28}{3} = -\frac{44}{3}$。所以点 P 对应的数为 4 或$-\frac{44}{3}$。
(4)当点 Q 开始运动后第 5，9，12.5 s 时，P，Q 两点之间距离为 4。
解析:点 P 运动到点 B 的时间为$[-10 - (-24)]÷1 = 14$（s），设在点 Q 开始运动后第$a$ s 时，P，Q 两点之间的距离为 4，当点 P 在点 Q 的右侧，且点 Q 还没追上点 P 时，$3a + 4 = 14 + a$，解得$a = 5$；
当点 P 在点 Q 的左侧，且点 Q 追上点 P 后，$3a - 4 = 14 + a$，解得$a = 9$；
当点 Q 到达点 C 后，且点 P 在点 Q 左侧时，$14 + a + 4 + 3a - 34 = 34$，解得$a = 12.5$。
综上，当点 Q 开始运动后第 5，9，12.5 s 时，P，Q 两点之间的距离为 4。