1. 数轴上的两个点表示的数为-3与a,并且$a > -3$,它们之间的距离可以表示为 (
D
)
A.$3 - a$
B.$-3 - a$
C.$a - 3$
D.$a + 3$
答案:D
解析:
解:数轴上两点之间的距离等于这两个点表示的数的差的绝对值。已知两个点表示的数为-3与a,且a>-3,所以它们之间的距离为|a - (-3)| = |a + 3|。因为a>-3,所以a + 3>0,|a + 3| = a + 3。
答案:D
2. 我们知道,若在数轴上,点A,B分别表示数a,b,则A,B之间的距离为$|a - b|$,已知点A,B,C,D,在数轴上分别表示数a,b,c,d,且$|a - c| = |b - c| = \frac{3}{2}|d - a| = 3(a ≠ b)$,则点C,D间的距离为____.
答案:5 或 1 解析:因为|a - c| = |b - c| = 3,所以点 C 在点 A 和点 B 之间.因为$\frac{3}{2}|d - a| = 3$,所以|d - a| = 2,不妨设点 A 在点 B 左侧,如图①:

点 C,D 间的距离为 5;如图②:

点 C,D 间的距离为 1.综上所述:点 C,D 间的距离为 5 或 1.
3. 已知数轴上有A,B两点,它们对应的数分别为1和-2.5,解答下面的问题:
(1)观察数轴,与点A的距离为4的点表示的数是
5 或-3
;
(2)数轴上有点C,且点C到点B的距离是点A到点B的距离的2倍,则点C表示的数是
4.5 或-9.5
;
(3)若将数轴折叠,使得点A与表示-3的点重合,求与点B重合的点表示的数.
因为点 A 到表示-3 的点的距离为|1 - (-3)| = 4,所以点 A 到折叠点的距离为 2,所以折叠点表示的数为-1,点 B 到表示-1 的点的距离为|-2.5 - (-1)| = 1.5,$-1 + 1.5 = 0.5$,所以与点 B 重合的点表示的数是 0.5.
答案:(1)5 或-3
(2)4.5 或-9.5 解析:点 A 到点 B 的距离为|1 - (-2.5)| = 3.5,所以点 C 到点 B 的距离为 7,$-2.5 - 7 = -9.5$,$-2.5 + 7 = 4.5$,故点 C 表示的数为 4.5 或-9.5.
(3)因为点 A 到表示-3 的点的距离为|1 - (-3)| = 4,所以点 A 到折叠点的距离为 2,所以折叠点表示的数为-1,点 B 到表示-1 的点的距离为|-2.5 - (-1)| = 1.5,$-1 + 1.5 = 0.5$,所以与点 B 重合的点表示的数是 0.5.
4. 数轴上点M表示有理数-3,将点M向右平移2个单位长度到达点N,点E到点N的距离为4,则点E表示的有理数为 (
B
)
A.3
B.-5或3
C.-9或-1
D.-1
答案:B
解析:
解:点M表示-3,向右平移2个单位得点N,
点N表示的数为:-3 + 2 = -1。
设点E表示的数为x,
∵点E到点N的距离为4,
∴|x - (-1)| = 4,即|x + 1| = 4。
当x + 1 = 4时,x = 3;
当x + 1 = -4时,x = -5。
点E表示的有理数为-5或3。
答案:B
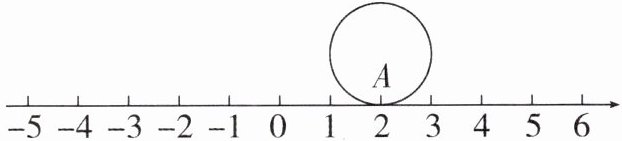
5. (2025·韶关期中)如图,直径为2的圆上有一点A,且点A与数轴上表示2的点重合,将这个圆在数轴上向左无滑动的滚动,当点A再次与数轴上的某个点重合时,这个点的位置可能在 (
D
)
A.8与9之间
B.7与8之间
C.-4与-3之间
D.-5与-4之间
答案:D 解析:因为这个圆在数轴上无滑动的滚动,所以滚动一周行进的距离为圆的周长(向左或者向右的距离).因为该圆的直径为 2,所以周长为$πd = π×2 = 2π$,所以将这个圆在数轴上向左无滑动的滚动,当点 A 再次与数轴上的某个点重合时,这个点可能为$2 - 2π$,因为$-5 < 2 - 2π < -4$,所以这个点的位置可能在-5 与-4 之间.故选 D.
6. 数轴上,点A的初始位置表示的数为2,现点A做如下移动:第1次点A向左移动1个单位长度至点$A_1$,第2次从点$A_1$向右移动2个单位长度至点$A_2$,第3次从点$A_2$向左移动3个单位长度至点$A_3$,…,按照这种移动方式进行下去,点$A_{2025}$表示的数是
-1011
.
答案:-1011 解析:第 n 次移动 n 个单位长度,则第 2025 次向左移动$2025×1$个单位长度,每左移右移各一次后,点 A 右移 1 个单位长度,所以$A_{2025}$表示的数是$2 + 1×(2024÷2) - 2025 = -1011$.
解析:
解:第1次移动后,点$A_1$表示的数为$2 - 1 = 1$;
第2次移动后,点$A_2$表示的数为$1 + 2 = 3$;
第3次移动后,点$A_3$表示的数为$3 - 3 = 0$;
第4次移动后,点$A_4$表示的数为$0 + 4 = 4$;
……
观察规律,每两次移动(一左一右)为一个循环,右移$2 - 1 = 1$个单位长度,循环结束后点表示的数为$2 + 1×k$($k$为循环次数)。
因为$2025$为奇数,前$2024$次移动共$2024÷2 = 1012$个循环,此时点表示的数为$2 + 1×1012 = 1014$。
第$2025$次为向左移动$2025$个单位长度,所以点$A_{2025}$表示的数是$1014 - 2025 = -1011$。
答案:$-1011$
7. 点A,B,C,D在数轴上的位置如图所示,已知点C,D之间的距离为2,点B,C之间的距离为5,点A,C之间的距离是点C,D之间距离的6倍.

(1)若点C为原点,则点A表示的数是____
-12
.
(2)若点P,Q分别从A,D两点同时出发,点P沿数轴正方向以每秒3个单位长度的速度向右运动,到达点C后立即按原速向点A折返;点Q沿数轴负方向以每秒1个单位长度的速度向左运动.当P,Q中的某点到达点A时,两点同时停止运动,设运动时间为t(单位:s).
①当$t = 3$时,点P与点Q之间的距离为____
2
;
②当$t = $____
$\frac{7}{2}$或5
时,点P与点Q相遇.
答案:(1)-12 解析:因为点 C,D 之间的距离为 2,点 A,C 之间的距离是点 C,D 之间距离的 6 倍,所以点 A,C 之间的距离是 12.因为点 C 为原点,所以点 A 表示的数是-12.
(2)①2 解析:因为点 A,C 之间的距离是 12,$12÷3 = 4(s)$,所以点 P 经过 4s 到达点 C,当$t = 3$时,点 A,P 之间的距离是 9,点 A,D 之间的距离是 14,所以此时点 A,Q 之间的距离是$14 - 1×3 = 11$,所以点 P 与点 Q 之间的距离为$11 - 9 = 2$.
②$\frac{7}{2}$ 或 5 解析:当$t < 4$或$t = 4$时,点 A,P 之间的距离是 3t,点 A,Q 之间的距离是$14 - t$,当$3t = 14 - t$时,点 P 与点 Q 相遇,得$t = \frac{7}{2}$;当$4 < t < 8$或$t = 8$时,点 A,P 之间的距离是$24 - 3t$,点 A,Q 之间的距离是$14 - t$,当$24 - 3t = 14 - t$时,点 P 与点 Q 相遇,得$t = 5$.综上,$t = \frac{7}{2}$或 5 时,点 P 与点 Q 相遇.