1. 已知数a,b,c在数轴上的位置如图所示,比较a,b,c,-a,-b,|c|,0的大小,并用“<”号将它们连接起来.
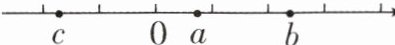
答案:在数轴上标出 -a,-b,|c|,可知 -b < c < -a < 0 < a < |c| < b.
解析:
解:由数轴可知,c<0<a<b,且|c|>b,|a|<b。
则 -a<0,-b<0,且 -b<c<-a。
所以 -b<c<-a<0<a<|c|<b。
2. 比较$-\frac {10}{13},-\frac {8}{9}$的大小.
答案:因为 $-\frac{10}{13}-(-\frac{8}{9})=-\frac{10}{13}+\frac{8}{9}=-\frac{90}{117}+\frac{104}{117}=\frac{14}{117}>0$,所以 $-\frac{10}{13}>-\frac{8}{9}$.
3. 若$x= -\frac {2022×2023}{2024×2025},y= -\frac {2022×2024}{2023×2025},z= -\frac {2022×2025}{2023×2024}$,比较x,y,z的大小.
答案:$\frac{x}{y}=-\frac{2022×2023}{2024×2025}×(-\frac{2023×2025}{2022×2024})=\frac{2023^{2}}{2024^{2}}<1$,又因为 x,y 均为负数,所以 $x > y$,同理,$\frac{y}{z}=\frac{2024^{2}}{2025^{2}}<1$,可得 $y > z$,所以 $x > y > z$.
解析:
解:$\frac{x}{y}=\left(-\frac{2022×2023}{2024×2025}\right)×\left(-\frac{2023×2025}{2022×2024}\right)=\frac{2023^{2}}{2024^{2}}<1$,
因为$x$,$y$均为负数,所以$x>y$;
$\frac{y}{z}=\left(-\frac{2022×2024}{2023×2025}\right)×\left(-\frac{2023×2024}{2022×2025}\right)=\frac{2024^{2}}{2025^{2}}<1$,
因为$y$,$z$均为负数,所以$y>z$;
综上,$x>y>z$。
4. 比较$\frac {1012}{2025}与\frac {1014}{2027}$的大小.
答案:因为 $\frac{1012}{2025}<\frac{1}{2}$ 且 $\frac{1}{2}<\frac{1014}{2027}$,所以 $\frac{1012}{2025}<\frac{1014}{2027}$.
解析:
解:因为 $2025×1 = 2025$,$1012×2 = 2024$,所以 $2024 < 2025$,即 $\frac{1012}{2025} < \frac{1}{2}$;
因为 $2027×1 = 2027$,$1014×2 = 2028$,所以 $2027 < 2028$,即 $\frac{1}{2} < \frac{1014}{2027}$;
所以 $\frac{1012}{2025} < \frac{1014}{2027}$。
5. 比较$-\frac {6}{23},-\frac {4}{17},-\frac {3}{11},-\frac {12}{47}$四个数的大小.
答案:通分使得分数的分子都为 12,即 $-\frac{6}{23}=-\frac{12}{46},-\frac{4}{17}=-\frac{12}{51},-\frac{3}{11}=-\frac{12}{44},-\frac{12}{47}=-\frac{12}{47}$,因为 $-\frac{12}{44}<-\frac{12}{46}<-\frac{12}{47}<-\frac{12}{51}$,所以 $-\frac{3}{11}<-\frac{6}{23}<-\frac{12}{47}<-\frac{4}{17}$.
解析:
解:将四个分数化为分子相同的分数:
$-\frac{6}{23}=-\frac{12}{46}$,$-\frac{4}{17}=-\frac{12}{51}$,$-\frac{3}{11}=-\frac{12}{44}$,$-\frac{12}{47}=-\frac{12}{47}$。
因为分子相同的负数,分母越大,分数值越大,所以:
$-\frac{12}{44}<-\frac{12}{46}<-\frac{12}{47}<-\frac{12}{51}$。
即:$-\frac{3}{11}<-\frac{6}{23}<-\frac{12}{47}<-\frac{4}{17}$。
6. 比较$\frac {5551}{5555},\frac {9215}{9219}$的大小.
答案:$\frac{5551}{5555}$ 的倒数是 $1\frac{4}{5551},\frac{9215}{9219}$ 的倒数是 $1\frac{4}{9215}$,因为 $1\frac{4}{5551}>1\frac{4}{9215}$,所以 $\frac{5551}{5555}<\frac{9215}{9219}$.
解析:
解:$\frac{5551}{5555}$的倒数是$1+\frac{5555-5551}{5551}=1\frac{4}{5551}$,
$\frac{9215}{9219}$的倒数是$1+\frac{9219-9215}{9215}=1\frac{4}{9215}$,
因为$5551<9215$,所以$\frac{4}{5551}>\frac{4}{9215}$,
则$1\frac{4}{5551}>1\frac{4}{9215}$,
所以$\frac{5551}{5555}<\frac{9215}{9219}$。
7. 设$a= \frac {19961995}{1995},b= \frac {19951996}{1996},c= \frac {19951996}{1995},d= \frac {19961995}{1996}$,比较a,b,c,d的大小.
答案:各数进行裂项,即 $a=\frac{19951995 + 10000}{1995}=10001+\frac{10000}{1995},b=\frac{19961996 - 10000}{1996}=10001-\frac{10000}{1996},c=\frac{19951995 + 1}{1995}=10001+\frac{1}{1995},d=\frac{19961996 - 1}{1996}=10001-\frac{1}{1996}$,因为 $\frac{10000}{1995}>\frac{1}{1995}>-\frac{1}{1996}>-\frac{10000}{1996}$,所以 $a > c > d > b$.
8. 已知a,b是有理数,且a,b异号,则$|a+b|,|a-b|,|a|+|b|$的大小关系为
$|a + b|<|a - b|=|a|+|b|$
.
答案:$|a + b|<|a - b|=|a|+|b|$ 解析:已知 a,b 异号,不妨取 $a = 2,b = - 1$ 或 $a = - 1,b = 2$.当 $a = 2,b = - 1$ 时,$|a + b|=|2+( - 1)|=1,|a - b|=|2-( - 1)|=3,|a|+|b|=|2|+| - 1|=3$;当 $a = - 1,b = 2$ 时,$|a + b|=| - 1 + 2|=1,|a - b|=| - 1 - 2|=3,|a|+|b|=| - 1|+|2|=3$,所以 $|a + b|<|a - b|=|a|+|b|$.
解析:
解:因为a,b异号,不妨设$a = 2$,$b=-1$,则$|a + b|=|2+(-1)| = 1$,$|a - b|=|2-(-1)| = 3$,$|a|+|b|=|2|+|-1| = 3$;
再设$a=-1$,$b = 2$,则$|a + b|=|-1 + 2| = 1$,$|a - b|=|-1-2| = 3$,$|a|+|b|=|-1|+|2| = 3$。
综上可得$|a + b|<|a - b|=|a|+|b|$。
故答案为:$|a + b|<|a - b|=|a|+|b|$