8. 若$|6 - x|与|y + 9|$互为相反数,则$x = $
6
,$y = $
-9
.
答案:6 -9
解析:
解:因为|6 - x|与|y + 9|互为相反数,所以|6 - x| + |y + 9| = 0。
又因为绝对值具有非负性,即|6 - x| ≥ 0,|y + 9| ≥ 0,所以只有当|6 - x| = 0且|y + 9| = 0时等式成立。
则6 - x = 0,解得x = 6;y + 9 = 0,解得y = -9。
x = 6,y = -9。
9. (1)当$x = $
3
时,$|x - 3| + 5$有最小值,为
5
.
(2)当$x = $
$-\frac{1}{2}$
时,$9 - |x + \frac{1}{2}|$有最大值,为
9
.
答案:(1)3 5 (2)$-\frac{1}{2}$ 9
解析:
(1)因为绝对值具有非负性,即$|x - 3| \geq 0$,当且仅当$x - 3 = 0$,即$x = 3$时,$|x - 3|$取得最小值$0$。所以当$x = 3$时,$|x - 3| + 5$有最小值,最小值为$0 + 5 = 5$。
(2)因为$|x + \frac{1}{2}| \geq 0$,所以$-|x + \frac{1}{2}| \leq 0$,当且仅当$x + \frac{1}{2} = 0$,即$x = -\frac{1}{2}$时,$-|x + \frac{1}{2}|$取得最大值$0$。所以当$x = -\frac{1}{2}$时,$9 - |x + \frac{1}{2}|$有最大值,最大值为$9 + 0 = 9$。
(1)3;5
(2)$-\frac{1}{2}$;9
10. 已知$|xy - 2|与|y - 1|$互为相反数,试求$\frac{1}{xy} + \frac{1}{(x + 1)(y + 1)} + \frac{1}{(x + 2)(y + 2)} + … + \frac{1}{(x + 2025)(y + 2025)}$的值.
答案:由题意得$|xy - 2| + |y - 1| = 0$,所以$xy = 2$,$y = 1$,所以$x = 2$,则原式=$\frac{1}{1×2} + \frac{1}{2×3} + \frac{1}{3×4} + \cdots + \frac{1}{2026×2027} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \cdots + \frac{1}{2026} - \frac{1}{2027} = 1 - \frac{1}{2027} = \frac{2026}{2027}$.
解析:
解:由题意得$|xy - 2| + |y - 1| = 0$,
因为绝对值为非负数,所以$xy - 2 = 0$且$y - 1 = 0$,
解得$y = 1$,代入$xy = 2$得$x = 2$。
则原式$=\frac{1}{2×1} + \frac{1}{(2+1)(1+1)} + \frac{1}{(2+2)(1+2)} + \cdots + \frac{1}{(2+2025)(1+2025)}$
$=\frac{1}{1×2} + \frac{1}{2×3} + \frac{1}{3×4} + \cdots + \frac{1}{2026×2027}$
$=1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \cdots + \frac{1}{2026} - \frac{1}{2027}$
$=1 - \frac{1}{2027}$
$=\frac{2026}{2027}$。
答案:$\frac{2026}{2027}$
11. (2025·武汉校级月考)【定义新知】
我们知道:式子$|x - 3|$的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离,因此,若点A,B在数轴上分别表示有理数a,b,则A,B两点之间的距离$AB = |a - b|$.若点P表示的数为x,请根据数轴解决以下问题:
(1)若$|x + 5| = 6$,则x的值为
1或-11
.
(2)当$|x + 3| + |x - 1|$取最小值时,x可以取整数
-3,-2,-1,0,1
;$|x + 3| - |x - 1|$的最大值为
4
.
(3)当$x = $
-2
时,$|x + 2| + |x + 6| + |x - 1|$的值最小,最小值为
7
.
(4)如图,一条笔直的公路边有三个居民区A,B,C和市民广场O,居民区A,B,C分别位于市民广场左侧5km,右侧1km,右侧3km.A居民区有居民1000人,B居民区有居民2000人,C居民区有居民3000人.现因物流需要,需要在该公路上建菜鸟驿站,用于接收这3个小区的快递,若快递的运输成本为1元/(千份·千米),那么菜鸟驿站建在何处才能使总运输成本最低,最低成本是多少?
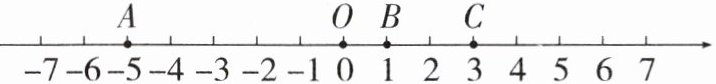
建在C居民区(3km处),最低成本12000元。
答案:(1) $|x + 5| = 6$表示数轴上点$x$与$-5$的距离为$6$,则$x + 5 = 6$或$x + 5=-6$,解得$x = 1$或$x=-11$。
(2) $|x + 3| + |x - 1|$表示点$x$到$-3$和$1$的距离之和,当$-3\leqslant x\leqslant1$时,距离之和最小,此时$x$可取整数$-3,-2,-1,0,1$;$|x + 3| - |x - 1|$,当$x\geqslant1$时,原式$=(x + 3)-(x - 1)=4$,为最大值。
(3) $|x + 2| + |x + 6| + |x - 1|$表示点$x$到$-6,-2,1$的距离之和,当$x=-2$时,距离之和最小,最小值为$|-2 + 6| + |-2 - 1|=4 + 3=7$。
(4) 设驿站在数轴上表示的数为$x$,总成本$y=1000|x + 5| + 2000|x - 1| + 3000|x - 3|$(单位:元)。当$x = 3$时,$y=1000×8 + 2000×2 + 3000×0=8000 + 4000=12000$元,此时成本最低。
(1) $1$或$-11$
(2) $-3,-2,-1,0,1$;$4$
(3) $-2$;$7$
(4) 建在$C$居民区($3km$处),最低成本$12000$元。