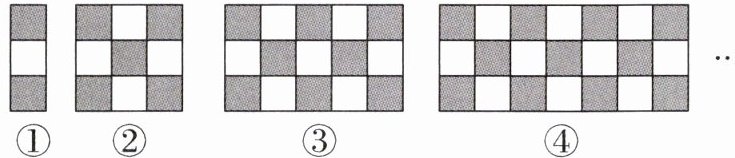
1.(2025·徐州期中)下列图形都是由几个灰色和白色的正方形按一定规律组成的,图①中有1个白色正方形,图②中有4个白色正方形,图③中有7个白色正方形,图④中有10个白色正方形……按此规律,图⑦中白色正方形的个数是(
C
)
A.23
B.20
C.19
D.17
答案:C
解析:
观察图形可知,图①中白色正方形个数为1,图②为4,图③为7,图④为10,相邻两图白色正方形个数相差3,即规律为:第n个图中白色正方形个数为$1 + 3(n - 1) = 3n - 2$。
当$n = 7$时,$3×7 - 2 = 19$。
答案:C
2.新趋势 跨学科融合 如图,一个钢球由静止开始从足够长的斜面顶端沿斜面滚下,其在斜面上经过的路程随时间变化规律如下表:|时间$t/s$|0|1|2|3|4|…$$|路程$s/m$|0|2|8|18|32|…$$|则小球从静止开始滚动10s,其经过的路程是(
D
)
A.40m
B.80m
C.160m
D.200m
答案:D
解析:
观察表格数据:
当$t=1$时,$s=2=2×1^{2}$;
当$t=2$时,$s=8=2×2^{2}$;
当$t=3$时,$s=18=2×3^{2}$;
当$t=4$时,$s=32=2×4^{2}$。
可得路程$s$与时间$t$的关系为$s = 2t^{2}$。
当$t = 10$时,$s=2×10^{2}=2×100 = 200$。
答案:D
3.(2024·哈尔滨校级模拟)小王利用计算机设计了一个计算程序,输入和输出的数据如表:
|输入|…$$|1|2|3|4|5|…$$|
|输出|…$$|$\frac{1}{2}$|$\frac{2}{5}$|$\frac{3}{10}$|$\frac{4}{17}$|$\frac{5}{26}$|…$$|
当输入数据为8时,输出的数据为
$\frac{8}{65}$
.
答案:$\frac{8}{65}$
解析:
观察输入与输出数据的关系:
当输入为1时,输出为$\frac{1}{2}=\frac{1}{1^2 + 1}$;
当输入为2时,输出为$\frac{2}{5}=\frac{2}{2^2 + 1}$;
当输入为3时,输出为$\frac{3}{10}=\frac{3}{3^2 + 1}$;
当输入为4时,输出为$\frac{4}{17}=\frac{4}{4^2 + 1}$;
当输入为5时,输出为$\frac{5}{26}=\frac{5}{5^2 + 1}$。
可得出规律:输入数据为$n$时,输出数据为$\frac{n}{n^2 + 1}$。
当输入数据为8时,输出数据为$\frac{8}{8^2 + 1}=\frac{8}{65}$。
$\frac{8}{65}$
4.(自贡中考改编)填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,$m$的值为
184
.
答案:184 解析:由前三个正方形中的四个数之间的关系可得最后一个正方形中的数分别为 11,13,15,m,因为 $3×5 - 1 = 14$;$5×7 - 3 = 32$;$7×9 - 5 = 58$,所以 $m = 13×15 - 11 = 184$。
解析:
观察前三个正方形中的数字规律:
左上角数字依次为1,3,5,均为奇数,且后一个比前一个大2,故最后一个正方形左上角为11时,右上角数字为11+2=13,左下角数字为13+2=15。
计算规律:$3×5 - 1 = 14$;$5×7 - 3 = 32$;$7×9 - 5 = 58$,即右上角数字×左下角数字 - 左上角数字 = 右下角数字。
因此,$m = 13×15 - 11 = 184$。
184
5.如图所示,一张纸片,小明第一次将其撕成四小片,手中共有4张纸片,以后每次都将其中一片撕成更小的四片……如此进行下去.
根据上述情况:
(1)当小明撕了4次后,共有
13
张纸片.
(2)当小明撕到第几次时,他手中共有76张纸片?
因为 $(76 - 1)÷3 = 25$ (次),所以当小明撕到第25次时,他手中共有76张纸片。
(3)小明说:“我撕了若干次后,手中的纸片有2025张.”小明说得对不对?若不对,请说出你的理由;若对,请求出小明撕了多少次.
不对.理由:因为 $(2025 - 1)÷3 = \frac{2024}{3}$,$\frac{2024}{3}$ 不是整数,所以小明说得不对。
答案:(1)13 解析:从题图中可以看出,当小明撕了 1 次时,手中有 $3×1 + 1 = 4$ (张) 纸片;当小明撕了 2 次时,手中有 $3×2 + 1 = 7$ (张) 纸片;当小明撕了 3 次时,手中有 $3×3 + 1 = 10$ (张) 纸片;当小明撕了 4 次时,手中有 $3×4 + 1 = 13$ (张) 纸片。 (2)因为 $(76 - 1)÷3 = 25$ (次),所以当小明撕到第 25 次时,他手中共有 76 张纸片。 (3)不对.理由:因为 $(2025 - 1)÷3 = \frac{2024}{3}$,$\frac{2024}{3}$ 不是整数,所以小明说得不对。
解析:
(1)13
(2)解:设撕了$n$次后有76张纸片,由规律得$3n + 1 = 76$,解得$n = (76 - 1)÷3 = 25$。答:第25次。
(3)解:假设对,设撕了$m$次,$3m + 1 = 2025$,$m=(2025 - 1)÷3 = 2024÷3$,结果不是整数。答:不对。
6.(2025·淄博期末)古希腊著名的毕达哥拉斯学派把1,3,6,10,…这样的数称为“三角形数”,而把1,4,9,16,…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是(
C
)

A.$13= 3+10$
B.$25= 9+16$
C.$36= 15+21$
D.$49= 18+31$
答案:C 解析:A.在 $13 = 3 + 10$ 中,13 不是“正方形数”,所以不符合题意;B.在 $25 = 9 + 16$ 中,9,16 不是“三角形数”,所以不符合题意;C.因为 $1 + 2 + 3 + 4 + 5 = 15$,$1 + 2 + 3 + 4 + 5 + 6 = 21$,所以 15,21 是两个相邻的“三角形数”。又因为 36 为“正方形数”,所以该选项符合题意;D.在 $49 = 18 + 31$ 中,18,31 不是“三角形数”,所以不符合题意.故选 C。
7.新趋势 数学文化 (2023·四川中考改编)在我国南宋数学家杨辉所著的《详解九章算法》(1261年)一书中,用如图的三角形解释二项和的乘方规律,因此我们称这个三角形为“杨辉三角”,根据规律第八行从左到右第三个数为(
C
)
A.7
B.16
C.21
D.35
答案:C 解析:根据规律可得第七行的数为 1,6,15,20,15,6,1,第八行的数为 1,7,21,35,35,21,7,1,所以根据规律第八行从左到右第三个数为 21.故选 C。