1. 将一张长方形纸对折,然后用笔尖在上面扎出“M”,再把它铺平,你见到的图形可能是(
A
)

答案:A
解析:
将长方形纸对折后扎出“M”,铺平后得到的图形关于折痕成轴对称。“M”本身左右对称,对折方式不影响其对称后的基本形状,符合轴对称特征的图形为选项A。
A
2. 某数学小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是 (
D
)
A.甲种方案所用铁丝最长
B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长
D.三种方案所用铁丝一样长
答案:D
解析:
解:设每个小正方形边长为1。
甲图形铁丝长度:通过平移,水平方向总长为4×2=8,竖直方向总长为3×2=6,总长度8+6=14。
乙图形铁丝长度:同理平移,水平方向总长为4×2=8,竖直方向总长为3×2=6,总长度8+6=14。
丙图形铁丝长度:同理平移,水平方向总长为4×2=8,竖直方向总长为3×2=6,总长度8+6=14。
三种方案所用铁丝长度均为14。
结论:D. 三种方案所用铁丝一样长。
3. (2025·甘肃期末)如图,将一个半径为 1 的圆形纸片连续对折三次之后,用剪刀沿虚线①剪开,可以得到一个三角形,内角和为 $ 180 ^ { \circ } $,则将该三角形展开后得到的多边形的内角和为 (
C
)
A.$ 180 ^ { \circ } $
B.$ 540 ^ { \circ } $
C.$ 1080 ^ { \circ } $
D.$ 2160 ^ { \circ } $
答案:C 解析:因为对折三次之后沿虚线剪开可以得到一个三角形,三角形内角和为 $180^{\circ}$,所以将该三角形展开后得到的多边形的内角和为 $180^{\circ} × 8 - 360^{\circ} = 1080^{\circ}$,故选 C。
4. 如图,观察月历,2025 年的国庆节是星期
三
.
答案:三 解析:根据 2025 年 6 月的月历知 7 月 1 日为星期二,7 月 1 日到国庆节还有 92 天,因为 $92 ÷ 7 = 13$(个)$\cdots\cdots1$(天),所以 2025 年国庆节是星期三。
解析:
解:由2025年6月月历知7月1日为星期二。
7月1日到10月1日(国庆节)的天数:31(7月)+31(8月)+30(9月)=92天。
$92÷7=13$(周)$\cdots\cdots1$(天)。
星期二往后推1天是星期三。
答:三
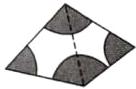
5. (1)有一块三角形的空地如图①所示,为了美化环境,现计划在以三角形各顶点为圆心,2m 长为半径的扇形区域(阴影部分)种上花草,那么种上花草的扇形区域总面积是______ $ m ^ { 2 } $.

(2)如图②,现需在一块四边形的空地上建造一个花园,要在以花园的四个顶点为圆心,2m 长为半径的扇形区域(阴影部分)种上花草,则种上花草的区域(阴影部分)的总面积是______ $ m ^ { 2 } $.
答案:(1) $2\pi$ 解析:因为三个扇形的圆心角的和为 $180^{\circ}$,所以 $S_{\text{阴影部分}} = \pi × 2^{2} × \frac{180^{\circ}}{360^{\circ}} = 2\pi$。
(2) $4\pi$ 解析:如图,将四边形沿虚线剪裁成 2 个三角形,所以原四个扇形就被分成 6 个扇形。所以以花园的四个顶点为圆心,2m 长为半径的扇形区域恰好能拼成一个完整的圆,所以 $S_{\text{阴影部分}} = \pi \cdot r^{2} = \pi \cdot 2^{2} = 4\pi(\text{m}^{2})$。
6. 观察如图所示的月历,解答下列问题:

(1)用长方形框去框月历里同一行的 4 个连续的数.若框里 4 个数的和是 66,则这 4 个数分别是多少?
(2)用一个 $ 4 × 3 $ 的长方形框去任意框 12 个数(如图),框里的 12 个数的和能等于 222 吗?能等于 246 吗?若能,请求出框里的 12 个数中的最小数;若不能,请说明理由.
答案:
(1) 令框里 4 个数中的最小数为 $x$,由题意得 $4x + 6 = 66$,解得 $x = 15$。所以其他三个数为 16,17,18,所以这 4 个数分别是 15,16,17,18。
(2) 令第一行的第一个数即最小的数是 $x$,则其他 11 个数分别为 $x + 1$,$x + 2$,$x + 3$,$x + 7$,$x + 8$,$x + 9$,$x + 10$,$x + 14$,$x + 15$,$x + 16$,$x + 17$,这 12 个数的和为 $x + (x + 1) + (x + 2) + (x + 3) + (x + 7) + (x + 8) + (x + 9) + (x + 10) + (x + 14) + (x + 15) + (x + 16) + (x + 17) = 12x + 102$。 当和为 222 时,$12x + 102 = 222$,解得 $x = 10$。此时,最小的数为 10。观察月历,能框出 12 个数的和等于 222。 当和为 246 时,$12x + 102 = 246$,解得 $x = 12$,此时,最小的数为 12。观察月历,不能框出 12 个数的和等于 246。
解析:
(1) 设框里 4 个数中的最小数为 $ x $,则其余三个数分别为 $ x+1 $,$ x+2 $,$ x+3 $。由题意得:
$ x + (x+1) + (x+2) + (x+3) = 66 $
$ 4x + 6 = 66 $
解得 $ x = 15 $
所以这 4 个数分别是 15,16,17,18。
(2) 设框里 12 个数中的最小数为 $ x $,则这 12 个数分别为 $ x $,$ x+1 $,$ x+2 $,$ x+3 $,$ x+7 $,$ x+8 $,$ x+9 $,$ x+10 $,$ x+14 $,$ x+15 $,$ x+16 $,$ x+17 $。它们的和为:
$ x + (x+1) + (x+2) + (x+3) + (x+7) + (x+8) + (x+9) + (x+10) + (x+14) + (x+15) + (x+16) + (x+17) = 12x + 102 $
当和为 222 时:
$ 12x + 102 = 222 $
解得 $ x = 10 $,能框出,最小数为 10。
当和为 246 时:
$ 12x + 102 = 246 $
解得 $ x = 12 $,不能框出。