8.(2025·无锡期中)“指间数”是一个很有趣的游戏,如图为手的示意图,在各个手指间标记字母A,B,C,D.请你按图中箭头所指方向(即$A\to B\to C\to D\to C\to B\to A\to B\to C…\to $的方式),从标记字母A开始数连续的正整数1,2,3,4,….当数到正整数2025时,对应的字母是
C
;当字母C第2025次出现时,恰好数到的数是
6075
.
答案:C 6075 解析:观察 $A→B→C→D→C→B→A→B→C→…$ 可知 $A→B→C→D→C→B$,6 个字母循环出现,因为 $2025÷6 = 337……3$,所以当数到 2025 时,对应的字母是 C;在每组循环内 C 出现 2 次, $2025÷2 = 1012$ (组) $……1$ (次),当字母 C 第 2025 次出现时,C 应在 $A→B→C$ 内,$1012×6 + 3 = 6075$,所以字母 C 第 2025 次出现时,恰好数到的数是 6075。
解析:
解:观察可得,字母按“$A→B→C→D→C→B$”的顺序循环出现,周期为6。
对于数到2025时对应的字母:
$2025÷6=337\cdots\cdots3$,其中余数为3,循环中的第3个字母是C,所以对应的字母是C。
对于字母C第2025次出现时对应的数:
每个周期内C出现2次,$2025÷2=1012\cdots\cdots1$,即经过1012个完整周期后,C第2025次出现是下一个周期中的第1次C,每个周期6个数,前1012个周期共有$1012×6$个数,下一个周期中第1次C出现在第3个数,所以恰好数到的数是$1012×6 + 3=6075$。
答案:C;6075
9.用同样大小的两种不同颜色的正方形纸片,按下图方式拼正方形.
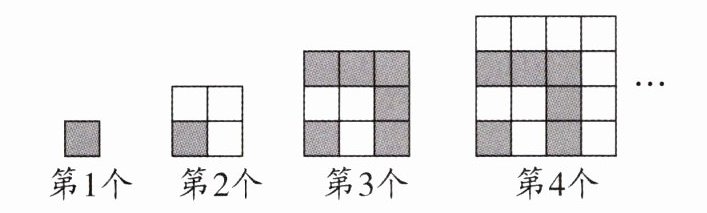
第1个图形中有1张正方形纸片;
第2个图形中有$1+3= 4$(张)正方形纸片;
第3个图形中有$1+3+5= 9$(张)正方形纸片;
第4个图形中有$1+3+5+7= 16$(张)正方形纸片;
……$ $
(1)根据上面的发现我们可以猜想:第5个图形中有
25
张正方形纸片(直接写出结果).
(2)请根据你的发现计算:
①$1+3+5+7+… +99= $
2500
;
②$101+103+105+… +199= $
7500
.
答案:
(1)25
(2)①2500 解析:设所求式子表示的是第 x 个图形中正方形纸片的张数,则 $2x - 1 = 99$,解得 $x = 50$,所以 $1 + 3 + 5 + 7 + … + 99 = 50² = 2500$。 ②7500 解析:$101 + 103 + 105 + … + 199 = (100 + 100 + 100 + … + 100) + (1 + 3 + 5 + 7 + … + 99) = 100×50 + 2500 = 7500$。
解析:
(1)25
(2)①2500
解:设所求式子表示第x个图形中正方形纸片的张数,
则2x-1=99,解得x=50,
所以1+3+5+7+…+99=50²=2500。
②7500
解:101+103+105+…+199
=(1+3+5+…+199)-(1+3+5+…+99)
设1+3+5+…+199为第y个图形,2y-1=199,解得y=100,其和为100²=10000,
所以原式=10000-2500=7500。
10.下面是一种利用图形计算正整数乘法的方法,根据图①~图④四个图形表示的规律,可知图⑤所表示的算式为
$21×13 = 273$
,图⑥所表示的算式为
$321×123 = 39483$
.
答案:$21×13 = 273$ $321×123 = 39483$ 解析:由已知图形,可知直线的数量和位置与两个乘数各个数位上的数有一定关系,从左上角至右下角各组直线的条数依次为第一个乘数由高到低各位上的数字,从左下角至右上角各组直线的条数依次为第二个乘数由高到低各位上的数字.从左向右的各区域内交点个数的和是积从高到低每一位上的数字.根据以上规律,题图⑤中算式可写为 $21×13 = 273$,题图⑥中算式可先写为 $321×123 = 38(14)83$,其中 14 大于 10,向前一位进 1,故前一位上加 1,即 $321×123 = 3(8 + 1)483$,算式为 $321×123 = 39483$。
解析:
图⑤所表示的算式为$21×13 = 273$,图⑥所表示的算式为$321×123 = 39483$。
11.意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和,现以这组数中的各个数作为正方形的边长构造正方形,再分别依次从左到右取2个、3个、4个、5个正方形拼成如下长方形并记为①,②,③,④,相应长方形的周长如下表:

|序号|①|②|③|④|
|周长|6|10|$x$|$y$|
(1)仔细观察图形,上表中的$x=$
16
,$y=$
26
.
(2)若按此规律继续作长方形,则序号为⑪的长方形周长是
754
.
答案:
(1)16 26
(2)754 解析:结合图形分析表格中图形的周长,第 1 个长方形的周长为 $(1 + 2)×2 = 6$;第 2 个长方形的周长为 $(2 + 3)×2 = 10$;第 3 个长方形的周长为 $(3 + 5)×2 = 16$;第 4 个长方形的周长为 $(5 + 8)×2 = 26$;第 5 个长方形的周长为 $(8 + 13)×2 = 42$;第 6 个长方形的周长为 $(13 + 21)×2 = 68$;第 7 个长方形的周长为 $(21 + 34)×2 = 110$;第 8 个长方形的周长为 $(34 + 55)×2 = 178$;第 9 个长方形的周长为 $(55 + 89)×2 = 288$;第 10 个长方形的周长为 $(89 + 144)×2 = 466$;所以第 11 个长方形的周长为 $(144 + 233)×2 = 754$。
解析:
(1)观察图形可知,斐波那契数列为1,1,2,3,5,8,13,…
第③个长方形由4个正方形拼成,边长为3和5,周长为$(3 + 5)×2 = 16$,故$x = 16$;
第④个长方形由5个正方形拼成,边长为5和8,周长为$(5 + 8)×2 = 26$,故$y = 26$。
(2)按规律依次计算:
第⑤个长方形边长8和13,周长$(8 + 13)×2 = 42$;
第⑥个边长13和21,周长$(13 + 21)×2 = 68$;
第⑦个边长21和34,周长$(21 + 34)×2 = 110$;
第⑧个边长34和55,周长$(34 + 55)×2 = 178$;
第⑨个边长55和89,周长$(55 + 89)×2 = 288$;
第⑩个边长89和144,周长$(89 + 144)×2 = 466$;
第⑪个边长144和233,周长$(144 + 233)×2 = 754$。
(1)16 26
(2)754