11. 新题型 新运算 (2024·泸州模拟)从n个不同元素中取出m个元素的所有不同组合的个数,叫作从n个不同元素中取出m个元素的组合数,用符号$C_{n}^{m}$表示.已知“!”是一种数学运算符号,且$1!= 1,2!= 2×1= 2,3!= 3×2×1= 6,4!= 4×3×2×1= 24,... $,若公式$C_{n}^{m}= \frac {n!}{m!(n-m)!}(n≥m,m,n$为正整数),则$C_{7}^{5}$为____
21
.
答案:21 解析:因为$C_{n}^{m}=\frac{n!}{m!(n-m)!}(n≥m$,n,m为正整数),所以$C_{7}^{5}=\frac{7!}{5!(7-5)!}=\frac{7×6×5×4×3×2×1}{5×4×3×2×1×2×1}=21$.
解析:
解:$C_{7}^{5}=\frac{7!}{5!(7-5)!}=\frac{7×6×5×4×3×2×1}{(5×4×3×2×1)×(2×1)}=\frac{5040}{120×2}=21$
答案:21
12. 计算:
(1)$[-2^{4}÷(-2\frac {2}{3})^{2}-\frac {11}{2}]÷\frac {1}{12};$
(2)$|-\frac {5}{7}|×(\frac {4}{5}-\frac {1}{3})÷(-\frac {2}{3})^{2}-(\frac {1}{2})^{2}.$
答案:(1)-93 (2)$\frac{1}{2}$
解析:
(1)解:原式$=[-16÷ \left(-\frac{8}{3}\right)^2-\frac{11}{2}]÷ \frac{1}{12}$
$=[-16÷ \frac{64}{9}-\frac{11}{2}]× 12$
$=[-16× \frac{9}{64}-\frac{11}{2}]× 12$
$=[-\frac{9}{4}-\frac{22}{4}]× 12$
$=(-\frac{31}{4})× 12$
$=-93$
(2)解:原式$=\frac{5}{7}× (\frac{12}{15}-\frac{5}{15})÷ \frac{4}{9}-\frac{1}{4}$
$=\frac{5}{7}× \frac{7}{15}× \frac{9}{4}-\frac{1}{4}$
$=\frac{1}{3}× \frac{9}{4}-\frac{1}{4}$
$=\frac{3}{4}-\frac{1}{4}$
$=\frac{1}{2}$
13. 有个写运算符号的游戏:在“$3□ (2□ 3)□ \frac {4}{3}□ 2^{2}$”中的每个$□$内填入“+”“-”“×”“÷”中的某一个(可重复使用),然后计算结果.
(1)请计算琪琪填入符号后得到的算式:$3×(2÷3)-\frac {4}{3}÷2^{2};$
$\frac{5}{3}$
(2)嘉嘉填入符号后得到的算式是$3÷(2×3)×\frac {4}{3}□ 2^{2}$,一不小心擦掉了$□$里的运算符号,但她知道结果是$-\frac {10}{3}$,请推算出$□$内的符号.
-
答案:(1)$3×(2÷3)-\frac{4}{3}÷2^{2}=3×(2÷3)-\frac{4}{3}×\frac{1}{4}=3×\frac{2}{3}-\frac{1}{3}=2-\frac{1}{3}=\frac{5}{3}$.(2)$3÷(2×3)×\frac{4}{3}□2^{2}=3÷6×\frac{4}{3}□2^{2}=\frac{2}{3}□4=-\frac{10}{3}$.因为$\frac{2}{3}-4=-\frac{10}{3}$,所以□里的符号应是“-”.
解析:
(1)解:$3×(2÷3)-\frac{4}{3}÷2^{2}$
$=3×\frac{2}{3}-\frac{4}{3}÷4$
$=2-\frac{4}{3}×\frac{1}{4}$
$=2-\frac{1}{3}$
$=\frac{5}{3}$
(2)解:$3÷(2×3)×\frac{4}{3}□2^{2}$
$=3÷6×\frac{4}{3}□4$
$=\frac{1}{2}×\frac{4}{3}□4$
$=\frac{2}{3}□4$
因为结果是$-\frac{10}{3}$,且$\frac{2}{3}-4=-\frac{10}{3}$,所以$□$内的符号是“$-$”。
14. 新考法 (2025·南通校级月考)取一个自然数,若它是奇数,则加上1,若它是偶数,则除以2,按此规则经过若干步的计算最终可得到1(注:计算到1结束).这个结论在数学上还没有得到证明,但举例验证都是正确的.例如,取自然数5,经过下面5步运算可得1,如图所示.如果自然数m恰好经过5步运算可得到1,那么所有符合条件的m的值有 (
C
)
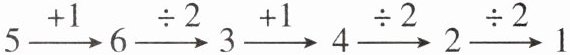
A.3个
B.4个
C.5个
D.6个
答案:C 解析:设自然数m为第一个数,经过1步运算得到的数为第二个数,以此类推,经过5步运算得到的1为第六个数,则第五个数为$1×2=2$,第四个数为$2×2=4$.①若第三个数是奇数,则第三个数为$4-1=3$,所以第二个数为$3×2=6$,所以第一个数$m=6-1=5$或$m=6×2=12$;②若第三个数是偶数,则第三个数为$4×2=8$,所以第二个数为$8×2=16$或$8-1=7$,所以第一个数$m=16-1=15$或$m=16×2=32$或$m=7×2=14$.综上,所有符合条件的m的值为5,12,14,15,32,共有5个.故选C.
15. 观察下列各式:
$1^{3}= 1= \frac {1}{4}×1^{2}×2^{2};$
$1^{3}+2^{3}= 9= \frac {1}{4}×2^{2}×3^{2};$
$1^{3}+2^{3}+3^{3}= 36= \frac {1}{4}×3^{2}×4^{2};$
$1^{3}+2^{3}+3^{3}+4^{3}= 100= \frac {1}{4}×4^{2}×5^{2};$
…
回答下面的问题:
(1)$1^{3}+2^{3}+3^{3}+4^{3}+5^{3}=$____
$\frac{1}{4}×5^{2}×6^{2}$
;
(2)计算$1^{3}+2^{3}+3^{3}+... +99^{3}+100^{3}$的值;
$1^{3}+2^{3}+3^{3}+... +99^{3}+100^{3}=\frac{1}{4}×100^{2}×101^{2}=25502500$
(3)计算$11^{3}+12^{3}+... +99^{3}+100^{3}$的值.
原式$=\frac{1}{4}×100^{2}×101^{2}-\frac{1}{4}×10^{2}×11^{2}=25502500-3025=25499475$
答案:(1)$\frac{1}{4}×5^{2}×6^{2}$(2)$1^{3}+2^{3}+3^{3}+... +99^{3}+100^{3}=\frac{1}{4}×100^{2}×101^{2}=25502500$.(3)原式$=\frac{1}{4}×100^{2}×101^{2}-\frac{1}{4}×10^{2}×11^{2}=25502500-3025=25499475$.
解析:
(1)$\frac{1}{4}×5^{2}×6^{2}$
(2)解:$1^{3}+2^{3}+3^{3}+... +99^{3}+100^{3}$
$=\frac{1}{4}×100^{2}×101^{2}$
$=\frac{1}{4}×10000×10201$
$=2500×10201$
$=25502500$
(3)解:$11^{3}+12^{3}+... +99^{3}+100^{3}$
$=(1^{3}+2^{3}+... +99^{3}+100^{3})-(1^{3}+2^{3}+... +10^{3})$
$=\frac{1}{4}×100^{2}×101^{2}-\frac{1}{4}×10^{2}×11^{2}$
$=25502500-\frac{1}{4}×100×121$
$=25502500-25×121$
$=25502500-3025$
$=25499475$