11. 平方等于它本身的数是,立方等于它本身的数是,平方等于它相反数的数是,立方等于它相反数的数是.

12. 观察下列算式: (1) $3^1= 3$, (2) $3^2= 9$, (3) $3^3= 27$, (4) $3^4= 81$, (5) $3^5= 243$, (6) $3^6= 729$, (7) $3^7= $ 2187 , (8) $3^8= 6561, …$. 根据算式中的规律, 你认为 $3^{100}$ 的个位数字是____.

13. 新题型 新定义 (2024·内江校级月考) 定义:如果$a^x= N(a＞0$, 且$a \neq 1)$, 那么 $x$ 叫作以 $a$ 为底 $N$ 的对数, 记作 $x= \log _a N$. 例如: 因为 $7^2= 49$, 所以 $\log _7 49= 2$; 因为 $5^3= 125$, 所以 $\log _5 125= 3$. 下列说法: (1) $\log _6 6= 36$; (2) $\log _3 81= $ 4; (3)若 $\log _4(a+14)= 2$, 则 $a= 2$; (4) $\log _2 64= $ $\log _2 32+\log _2 2$. 正确的有____(填序号).

14. 阅读下列各式: $(a × b)^2= a^2 × b^2,(a × b)^3= a^3 ×$ $b^3,(a × b)^4= a^4 × b^4,(a × b)^5= a^5 × b^5 … …$
回答下列问题:
(1) 猜想: $(a × b)^n= $.
(2) 请用我们学过的知识说明上式成立的理由.

(3) 请计算:
(1) $\left(-\frac{1}{4}\right)^{1000} × 4^{1000}$;

(2) $(-0.125)^{2025} × 2^{2024} × 4^{2023}$.

15. (2025·深圳期中) 在一次综合实践活动课上, 张老师给每位同学各发了一张正方形纸片, 请同学们思考如何通过折纸的方法求出 $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+…+\frac{1}{2^6}$ 的值.
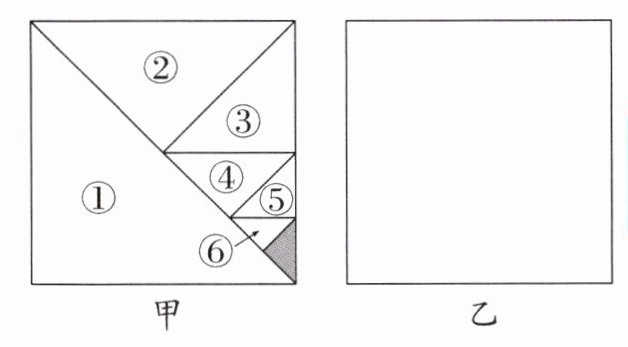
【操作探究】“乘风”小组的同学经过一番思考和讨论交流后, 进行了如下操作: 如图甲, 将一个边长为 1 的正方形纸片分割成 7 个部分, 第(1)部分是边长为 1 的正方形纸片面积的一半, 第(2)部分是第(1)部分面积的一半, 第(3)部分是第(2)部分面积的一半……依次类推, 则图甲中空白部分的面积为 $\frac{1}{2}+\frac{1}{4}+$ $\frac{1}{8}+…+\frac{1}{2^6}$.
“破浪”小组是这样思考的: 设 $S= \frac{1}{2}+\frac{1}{4}+$ $\frac{1}{8}+…+\frac{1}{2^6}$,
将等式两边同时乘 $\frac{1}{2}$ 得 $\frac{1}{2} S= \frac{1}{4}+\frac{1}{8}+…+$ $\frac{1}{2^6}+\frac{1}{2^7}$,
将上式减去下式得 $\frac{1}{2} S= \frac{1}{2}-\frac{1}{2^7}$, 即 $S= 1-\frac{1}{2^6}= $ $\frac{63}{64}$, 即 $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+…+\frac{1}{2^6}= \frac{63}{64}$.
甲
乙

【过程思考】
(1) 图甲中阴影部分的面积是____, $\frac{1}{2}+$ $\frac{1}{4}+\frac{1}{8}+…+\frac{1}{2^7}= $____.
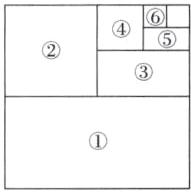
(2) 请你利用图乙, 再设计能求 $\frac{1}{2}+\frac{1}{4}+$ $\frac{1}{8}+…+\frac{1}{2^6}$ 的值的几何图形. (只画出图形即可)
(3) 根据以上规律, 计算:
(1) $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+…+\frac{1}{2^n}= $____; ( $n$ 为正整数)
(2) $2+4+8+16+…+2^n= $____. ( $n$ 为正整数)