10. (2025·杭州校级月考)如图,数轴上点A,B,C,D所表示的数分别是a,b,c,d,若$abcd<0$,$ab>cd$,则原点的位置在 (
D
)
A.点A的左边
B.A,B两点之间
C.B,C两点之间
D.C,D两点之间
答案:D解析:因为$abcd<0,a<b<c<d$,所以$a<0,b,c,d>0$或$a,b,c<0,d>0$.因为$ab>cd$,所以$a,b,c<0,d>0$.所以原点的位置在C,D两点之间.故选D.
11. (1)已知$|x|= 3,|y|= 2$,且$x+y>0$,则$xy= $
$\pm 6$
;
(2)若$|a|= 3,|-b|= 7$,且$ab>0$,则$a-b= $
$\pm 4$
.
答案:(1)$\pm 6$解析:由题意可得$x=3,y=\pm 2$,故$xy=\pm 6$. (2)$\pm 4$解析:由题意可得$a=3,b=7$或$a=-3,b=-7$,故$a-b=\pm 4$.
解析:
(1)解:因为$|x| = 3$,所以$x = \pm 3$;因为$|y| = 2$,所以$y = \pm 2$。
又因为$x + y>0$,当$x = 3$时,$y = 2$或$y=-2$均满足;当$x=-3$时,$y = 2$或$y=-2$均不满足。所以$x = 3$,$y = \pm 2$。
则$xy = 3×2 = 6$或$xy = 3×(-2) = -6$,故$xy = \pm 6$。
(2)解:因为$|a| = 3$,所以$a = \pm 3$;因为$|-b| = 7$,所以$|b| = 7$,即$b = \pm 7$。
又因为$ab>0$,所以$a$,$b$同号。当$a = 3$时,$b = 7$;当$a=-3$时,$b=-7$。
则$a - b = 3 - 7 = -4$或$a - b=-3 - (-7)=4$,故$a - b = \pm 4$。
12. 小海在自学了简单的电脑编程后,设计了如图所示的程序,若他输入的数是2,则执行程序后,输出的数是
−558
.
答案:−558解析:第一次输入后,计算得$(2-8)×9=-54,|-54|<100$;第二次输入后,计算得$(-54-8)×9=-558,|-558|>100$,故输出的数是−558.
解析:
第一次输入2:
$(2 - 8)×9 = -54$,$|-54| = 54 < 100$;
第二次输入$-54$:
$(-54 - 8)×9 = -558$,$|-558| = 558 > 100$,输出$-558$。
$-558$
13. (2025·无锡校级月考)某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
|与标准质量的差值(单位:g)|-5|-2|0|1|3|6|
|袋数|1|4|3|4|5|3|
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若标准质量为450g,则抽样检测的20袋食品的总质量为多少克?
(3)若该种食品的合格标准为$450\pm 5g$,求该食品的抽样检测的合格率.
答案:(1)与标准质量的差值的和为$(-5)×1+(-2)×4+0×3+1×4+3×5+6×3=24$,其平均数为$24÷20=1.2$,即这批样品的平均质量比标准质量多,多1.2g. (2)总质量为$450×20+24=9000+24=9024(g)$.答:抽样检测的20袋食品的总质量为9024g. (3)因为合格的有$1+4+3+4+5=17$(袋),所以食品的合格率为$\frac{17}{20}×100\% =85\% $.答:该食品的抽样检测的合格率为85%.
解析:
(1)与标准质量的差值的和为$(-5)×1+(-2)×4+0×3+1×4+3×5+6×3=24$,其平均数为$24÷20=1.2$,即这批样品的平均质量比标准质量多,多$1.2$克。
(2)总质量为$450×20+24=9000+24=9024$克。
(3)合格的袋数为$1+4+3+4+5=17$袋,合格率为$\frac{17}{20}×100\% =85\% $。
答:(1)这批样品的平均质量比标准质量多,多$1.2$克;(2)抽样检测的20袋食品的总质量为9024克;(3)该食品的抽样检测的合格率为$85\% $。
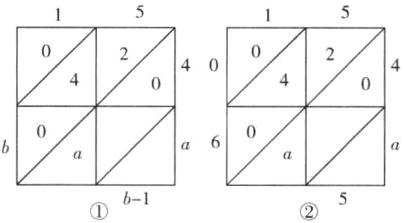
14. 新趋势 数学文化 “格子乘法”作为两个数相乘的一种计算方法最早在15世纪由意大利数学家帕乔利提出,在明代的《算法统宗》一书中被称为“铺地锦”,如图①,计算$47×51$,将乘数47计入上行,乘数51计入右行,然后以乘数47的每位数字乘51的每位数字,将结果计入相应的格子中,最后按斜行加起来(斜行的和均小于10),得2397.如图②,用“铺地锦”的方法表示两个两位数相乘,这两个两位数相乘的结果为____.
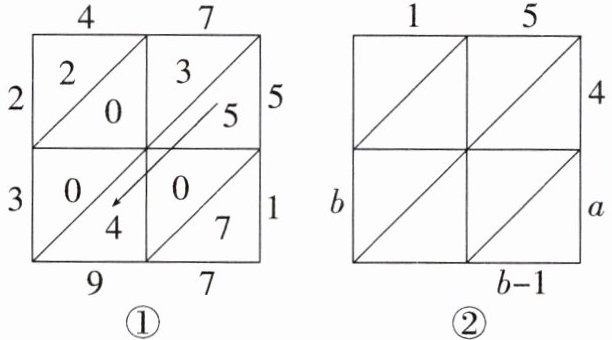
答案:615或645或675解析:$1×4=4,5×4=20,1\cdot a=a$,所以如图①,易得$b=6$,所以由图②得a应为奇数1,3,5,7,9中的一个.所以两个两位数可以为$15×41;15×43;15×45;15×47;15×49$,所以相乘结果为615或645或675或705或735.由题意,斜行的和均小于10,当a为7或9时,不符合题意,所以相乘结果705和735舍去.故答案为615或645或675.
15. 计算:
(1)$(1-\frac {1}{2})×(\frac {1}{3}-1)×(1-\frac {1}{4})×(\frac {1}{5}-1)×... ×(1-\frac {1}{2024})×(\frac {1}{2025}-1)$;
(2)$(\frac {1}{2}+1)×(\frac {1}{3}-1)×(\frac {1}{4}+1)×(\frac {1}{5}-1)×... ×(\frac {1}{2024}+1)×(\frac {1}{2025}-1)$;
(3)$(1+\frac {1}{3})×(1+\frac {1}{8})×(1+\frac {1}{15})×... ×(1+\frac {1}{99})$.
答案:(1)原式$=\frac{1}{2}×(-\frac{2}{3})×\frac{3}{4}×(-\frac{4}{5})×... ×\frac{2023}{2024}×(-\frac{2024}{2025})=\frac{1}{2025}$. (2)原式$=\frac{3}{2}×(-\frac{2}{3})×\frac{5}{4}×(-\frac{4}{5})×... ×\frac{2025}{2024}×(-\frac{2024}{2025})=\underbrace{(-1)×(-1)×... ×(-1)}_{共1012个(-1)}=1$. (3)原式$=\frac{4}{3}×\frac{9}{8}×\frac{16}{15}×... ×\frac{100}{99}=\frac{2^{2}}{1×3}×\frac{3^{2}}{2×4}×\frac{4^{2}}{3×5}×... ×\frac{10^{2}}{9×11}=\frac{2×10}{1×11}=\frac{20}{11}$.