10. 计算:
(1)$(-5\frac {1}{4})-(0-1\frac {1}{4})-(+6\frac {13}{20})$;
(2)$|(-61)-(-71)|-|2-8|$;
(3)$|-4\frac {1}{4}-(-4\frac {3}{4})|-(|-4\frac {1}{4}|-|-4\frac {3}{4}|)$.
答案:(1) 原式$=-5\frac{1}{4}-(-1\frac{1}{4})-6\frac{13}{20}=-4-6\frac{13}{20}=-10\frac{13}{20}$. (2) 原式$=|(-61)+71|-| - 6|=10 - 6 = 4$. (3) 原式$=\frac{1}{2}-(4\frac{1}{4}-4\frac{3}{4})=\frac{1}{2}-(-\frac{1}{2}) = 1$.
解析:
(1)解:原式$=-5\frac{1}{4}-(-1\frac{1}{4})-6\frac{13}{20}$
$=-5\frac{1}{4}+1\frac{1}{4}-6\frac{13}{20}$
$=-4-6\frac{13}{20}$
$=-10\frac{13}{20}$
(2)解:原式$=|(-61)+71|-|2-8|$
$=|10|-|-6|$
$=10-6$
$=4$
(3)解:原式$=|-4\frac{1}{4}+4\frac{3}{4}|-(\left| -4\frac{1}{4} \right|-\left| -4\frac{3}{4} \right|)$
$=\left| \frac{1}{2} \right|-(4\frac{1}{4}-4\frac{3}{4})$
$=\frac{1}{2}-(-\frac{1}{2})$
$=\frac{1}{2}+\frac{1}{2}$
$=1$
11. (2025·徐州期中)【阅读理解】小明发现,不计算结果,也可根据绝对值的性质去掉绝对值符号,如:$|6+7|= 6+7;|6-7|= 7-6;|7-6|= 7-6;|-6-7|= 6+7$.
【尝试应用】根据上述规律,去掉下列各式的绝对值符号:
(1)$|4-13|=$
$13 - 4$
;
(2)$|\frac {2}{3}-\frac {3}{4}|=$
$\frac{3}{4}-\frac{2}{3}$
.
【深入研究】有理数a,b在数轴上的位置如图所示,则$|3a+2b|=$
$-3a - 2b$
.
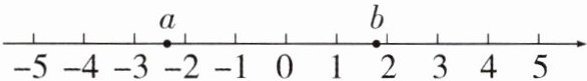
【解决问题】用简便的方法计算:
$|\frac {1}{2}-1|+|\frac {1}{3}-\frac {1}{2}|+... +|\frac {1}{4}-\frac {1}{3}|+|\frac {1}{5}-\frac {1}{4}|+... +|\frac {1}{2025}-\frac {1}{2024}|=$
$\frac{2024}{2025}$
.
答案:【尝试应用】(1) $13 - 4$ (2) $\frac{3}{4}-\frac{2}{3}$ 【深入研究】$-3a - 2b$ 解析:根据题中数轴中a,b的位置得$a<0,b>0$,所以$3a<0,2b>0$,因为$|a|>|b|$,所以$3a + 2b<0$,所以$|3a + 2b|=-3a - 2b$. 【解决问题】$\frac{2024}{2025}$ 解析:原式$=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\cdots+\frac{1}{2024}-\frac{1}{2025}=1-\frac{1}{2025}=\frac{2024}{2025}$.
解析:
【尝试应用】
(1) $13 - 4$
(2) $\frac{3}{4} - \frac{2}{3}$
【深入研究】
$-3a - 2b$
【解决问题】
$\frac{2024}{2025}$
12. 阅读下面材料:
有依次排列的3个数:3,9,8,对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:3,6,9,-1,8,这称为第一次操作;第二次同样的操作后也可产生一个新数串:3,3,6,3,9,-10,-1,9,8;继续依次操作下去.
(1)有依次排开的3个数:3,-5,7,第一次操作后,增加的所有新数之和是多少?
(2)在(1)的前提下,经过第二次操作后所得的新数串比第一次操作后所得的数串增加的所有新数之和是多少?
(3)猜想:有依次排开的3个数a,b,c,第一百次操作后得到的新数串比第九十九次操作后所得的数串增加的所有新数之和是多少?
答案:(1) 第一次操作后增加的新数是-8,12,则增加的所有新数之和为$-8 + 12 = 4$. (2) 第二次操作后所得的新数串比第一次操作后所得的数串增加的所有新数之和为$-11 + 3 + 17 - 5 = 4$. (3) 猜想:第一百次操作后得到的新数串比第九十九次操作后所得的数串增加的所有新数之和为$-a + c$.
解析:
(1) 原数串:3,-5,7。第一次操作后新数串:3,-8,-5,12,7。增加的新数为-8,12。增加的所有新数之和:-8+12=4。
(2) 第一次操作后数串:3,-8,-5,12,7。第二次操作后新数串:3,-11,-8,3,-5,17,12,-5,7。增加的新数为-11,3,17,-5。增加的所有新数之和:-11+3+17-5=4。
(3) -a+c