8. (2025·益阳期末)已知数轴上点A,B的位置如图所示,点A表示的有理数为$a$,点B表示的有理数为$b$,$m = a + b$,则比$m$大的最小整数为(
B
)
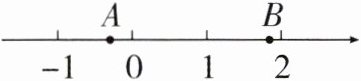
A.$1$
B.$2$
C.$3$
D.$4$
答案:B 解析:由题图得,$-\frac{1}{2} < a < 0$,$\frac{3}{2} < b < 2$,所以 $1 < a + b < 2$. 因为 $m = a + b$,所以 $1 < m < 2$,比 $m$ 大的最小整数为 2. 故选 B.
9. 若非零数$a$,$b满足| a + b | = | a | + | b |$,则(
D
)
A.$a$,$b$均为正数
B.$a$,$b$均为负数
C.$a$,$b$异号
D.$a$,$b$同号
答案:D 解析:当 $a$,$b$ 均为正数时,$|a + b| = a + b$,$|a| + |b| = a + b$,满足题意;当 $a$,$b$ 均为负数时,$|a + b| = -a - b$,$|a| + |b| = -a - b$,即 $|a + b| = |a| + |b|$,满足题意;当 $a$ 为正数,$b$ 为负数时,$|a + b| = a + b$ 或 $|a + b| = -a - b$,$|a| + |b| = a - b$,两者不相等,不符合题意;同理可知,当 $a$ 为负数,$b$ 为正数时,不符合题意. 综上,$a$,$b$ 同号等式成立,故选 D.
10. 小颖同学做这样一道题:计算$| - 4 + \triangle |$.其中“$\triangle$”是被墨水污染看不清的一个数,她翻开后面的答案,得知该题的计算结果是$3$,那么“$\triangle$”表示的数是
7 或 1
.
答案:7 或 1 解析:由题可知,$|-4 + \triangle| = 3$,即 $-4 + \triangle = 3$ 或 $-4 + \triangle = -3$,解得 $\triangle = 7$ 或 $\triangle = 1$.
解析:
解:由题意得,$|-4 + \triangle| = 3$,
则 $-4 + \triangle = 3$ 或 $-4 + \triangle = -3$,
当 $-4 + \triangle = 3$ 时,解得 $\triangle = 7$;
当 $-4 + \triangle = -3$ 时,解得 $\triangle = 1$。
故“$\triangle$”表示的数是 7 或 1。
11. 新题型 新定义 设用符号$( a , b )表示a$,$b$两数中较小的数,用符号$[ a , b ]表示a$,$b$两数中较大的数,试求下列各式的值.
(1)$( - 5 , - 0.5 ) + [ - 4,2 ] = $
-3
.
(2)$\left( - 1 \frac { 1 } { 2 } , 3 \right) + \left[ - 4 , \left( - \frac { 11 } { 3 } , - 7 \right) \right] =$
$-5\frac{1}{2}$
.
答案:(1)-3 解析:$(-5, -0.5) + [-4, 2] = -5 + 2 = -3$. (2)$-5\frac{1}{2}$ 解析:$\left(-1\frac{1}{2}, 3\right) + \left[-4, \left(-\frac{11}{3}, -7\right)\right] = -1\frac{1}{2} + [-4, -7] = -1\frac{1}{2} + (-4) = -5\frac{1}{2}$.
12. (1)已知$| a | = 5$,$| b | = 2$,且$a > b$,则$a + b$的值为
7 或 3
.
(2)已知$| a | = 4$,$| b | = 3$,且$| a - b | = b - a$,则$a + b$的值为
-1 或 -7
.
答案:(1)7 或 3 解析:因为 $|a| = 5$,$|b| = 2$,且 $a > b$,所以 $a = 5$,$b = \pm 2$,故 $a + b = 7$ 或 $a + b = 3$. (2)-1 或 -7 解析:因为 $|a| = 4$,$|b| = 3$,所以 $a = \pm 4$,$b = \pm 3$. 因为 $|a - b| = b - a$,所以 $a - b \leq 0$,即 $a \leq b$,所以当 $a = -4$,$b = -3$ 时,$a + b = -4 + (-3) = -7$,当 $a = -4$,$b = 3$ 时,$a + b = -4 + 3 = -1$. 综上,$a + b$ 的值为 -1 或 -7.
解析:
(1)
解:∵|a|=5,|b|=2,
∴a=±5,b=±2.
∵a>b,
∴a=5,b=2或a=5,b=-2.
当a=5,b=2时,a+b=5+2=7;
当a=5,b=-2时,a+b=5+(-2)=3.
∴a+b的值为7或3.
(2)
解:∵|a|=4,|b|=3,
∴a=±4,b=±3.
∵|a-b|=b-a,
∴a-b≤0,即a≤b.
∴a=-4,b=3或a=-4,b=-3.
当a=-4,b=3时,a+b=-4+3=-1;
当a=-4,b=-3时,a+b=-4+(-3)=-7.
∴a+b的值为-1或-7.
13. (2025·唐山期末)我国自主研发的巡逻机器人备受关注,为安保工作提供了强有力的支持.某天小明发现一个巡逻机器人正准备在一条南北方向的公路上执行治安巡逻.(规定初始位置为$0$,向北走为正,向南走为负)它从初始位置到结束巡逻所走的路程(单位:$\mathrm { km }$)如下:
|次数|第一次|第二次|第三次|第四次|第五次|第六次|
|路程/$\mathrm { km }$|$+ 2$|$- 1.5$|$+ 4.5$|$- 2$|$+ 0.5$|$- 1.5$|
(1)直接写出巡逻机器人在这次巡逻中离出发点最远的距离为____$\mathrm { km }$;
(2)通过计算,描述巡逻机器人结束巡逻时的最后位置;
(3)已知这次巡逻机器人的平均速度为$3 \mathrm { km } / \mathrm { h }$,请求出巡逻机器人的巡逻时间.
(1)
5
(2)
$+2 - 1.5 + 4.5 - 2 + 0.5 - 1.5 = 2(km)$,所以巡逻机器人结束巡逻时的最后位置在出发点北面 2 km 处.
(3)
此次巡逻共走 $|+2| + |-1.5| + |+4.5| + |-2| + |+0.5| + |-1.5| = 12(km)$,$12 ÷ 3 = 4(h)$,所以巡逻机器人的巡逻时间是 4 h.
答案:(1)5 解析:第一次:+2 km;第二次:$+2 - 1.5 = 0.5(km)$;第三次:$0.5 + 4.5 = 5(km)$;第四次:$5 - 2 = 3(km)$;第五次:$3 + 0.5 = 3.5(km)$;第六次:$3.5 - 1.5 = 2(km)$;所以巡逻机器人在这次巡逻中离出发点最远的距离为 5 km. (2)$+2 - 1.5 + 4.5 - 2 + 0.5 - 1.5 = 2(km)$,所以巡逻机器人结束巡逻时的最后位置在出发点北面 2 km 处. (3)此次巡逻共走 $|+2| + |-1.5| + |+4.5| + |-2| + |+0.5| + |-1.5| = 12(km)$,$12 ÷ 3 = 4(h)$,所以巡逻机器人的巡逻时间是 4 h.
解析:
(1)5
(2)解:+2 - 1.5 + 4.5 - 2 + 0.5 - 1.5 = 2(km)
答:巡逻机器人结束巡逻时的最后位置在出发点北面2km处。
(3)解:|+2| + |-1.5| + |+4.5| + |-2| + |+0.5| + |-1.5| = 12(km)
12 ÷ 3 = 4(h)
答:巡逻机器人的巡逻时间是4h。
14. 小丽在$4$张同样的纸片上各写了一个正整数,从中随机抽取$2$张,并将它们上面的数相加.重复这样做,每次所得的和都是$5$,$6$,$7$,$8$中的一个数,并且这$4$个数都能取到.猜猜看,小丽在$4$张纸片上各写下的数是
2, 3, 3, 5 或 2, 3, 4, 4
.
答案:2, 3, 3, 5 或 2, 3, 4, 4 解析:若这 4 个数从小到大排列分别为 $a$,$b$,$c$,$d$. ①当 4 个数中最小的数 $a$ 为 1 时,因为 $1 + 4 = 5$,所以 $b = 4$. 因为 $1 + 5 = 6$,$4 + 2 = 6$,所以 $c$ 只能为 5,此时 $b + c = 9$,不符合题意. ②当 4 个数中最小的数 $a$ 为 2 时,因为 $2 + 3 = 5$,所以 $b = 3$. 因为 $2 + 4 = 6$,$3 + 3 = 6$,所以 $c = 3$ 或 $c = 4$,当 $c = 3$ 时,$d = 5$,当 $c = 4$ 时,$d = 4$. ③当 4 个数中最小的数 $a$ 为 3 或大于 3 的整数时,无法得出和为 5 的结果,不符合题意. 综上所述,四个数分别为 2, 3, 3, 5 或 2, 3, 4, 4.
解析:
解:设这4个数从小到大排列分别为$a$,$b$,$c$,$d$。
1. 最小和为$a + b = 5$,最大和为$c + d = 8$。
2. 当$a = 2$时,$b = 3$。
若$c = 3$,则$d = 8 - 3 = 5$,此时数为2,3,3,5,可得到和5(2+3)、6(3+3)、7(2+5)、8(3+5)。
若$c = 4$,则$d = 8 - 4 = 4$,此时数为2,3,4,4,可得到和5(2+3)、6(2+4)、7(3+4)、8(4+4)。
3. 当$a \geq 3$时,无法得到和5,不符合题意。
结论:2,3,3,5 或 2,3,4,4。
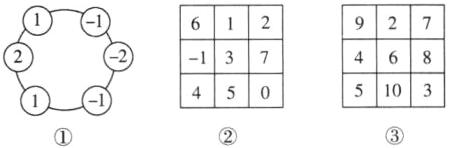
15. 还记得小时候经常玩的填数游戏吗?一起用有理数来试试吧!
(1)请在图①的各个圆圈内填上适当的数,使每个圆圈内的数都等于与它相邻的两个数的和;
(2)如图②,在$3 × 3$的方格中补全数字,使得每行、每列、每条对角线上的三个数之和相等;
(3)如图③,请将$2$,$3$,$4$,$5$,$6$,$7$,$8$,$9$,$10填入3 × 3$的方格中,使得每行、每列、每条对角线上的三个数之和相等.

答案:(1)如图①所示 (2)$2 + 3 + 4 = 9$,则每行、每列、每条对角线上的三个数之和均为 9,所填结果如图②所示 (3)因为 $2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 54$,所以三行所有数的和为 54,所以每一行的三个数之和为 18,类比(2)中的规律,中间格应填 6,相加等于 12 的两个数对称排列,如图③所示. (答案不唯一)