1. (2024·无锡期末)定义一种新运算:$a\oplus b= 2a+b,a※b= a^{2}b$,则方程$(x+1)\oplus 2= (3※x)-2$的解是 (
C
)
A.$x= \frac {5}{2}$
B.$x= -1$
C.$x= \frac {6}{7}$
D.$x= 2$
答案:1. C 解析:因为 $ a \oplus b = 2a + b $,$ a ※ b = a ^ { 2 } b $,$ ( x + 1 ) \oplus 2 = ( 3 ※ x ) - 2 $,所以 $ 2 ( x + 1 ) + 2 = 3 ^ { 2 } \cdot x - 2 $,整理得 $ 7 x = 6 $,解得 $ x = \frac { 6 } { 7 } $。故选 C。
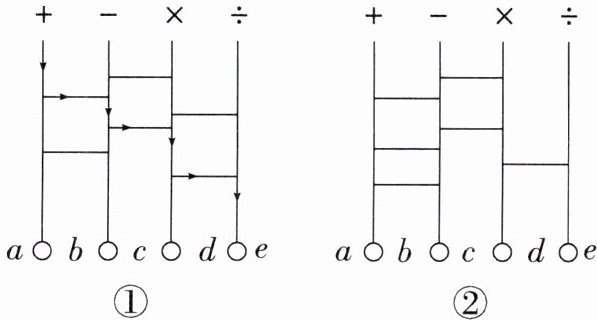
2. 新考法(2024·无锡期末)图①中每相邻两条线间,有从上至下的几条横线(即“桥”),这样就构成了“天梯”.运算符号“+,-,×,÷”在“天梯”的竖线与横线上运动,它们在运动的过程中按自上而下,且逢“桥”必过的规则进行,最后运动到竖线下方的“○”中,将a,b,c,d,e连接起来,构成一个算式.如:“+”号根据规则就应该沿图中箭头方向运动,最后向下进入“○”中,其余3个运算符号分别按规则运动到“○”中后,就得到算式$a÷b×c-d+e$.根据如图②所示的“天梯”计算当$a= -6,b= -1.5^{2},c= -2,d= \frac {3}{4},e= -\frac {2}{3}$时所写算式的结果为 ( )
A.$\frac {31}{2}$
B.$-\frac {23}{2}$
C.$\frac {23}{2}$
D.$-\frac {31}{2}$
答案:2. A 解析:由题意确定各符号的位置,
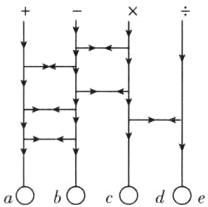
此时的算式为 $ a × b - c ÷ d + e $,当 $ a = - 6 $,$ b = - 1.5 ^ { 2 } $,$ c = - 2 $,$ d = \frac { 3 } { 4 } $,$ e = - \frac { 2 } { 3 } $时,$ a × b - c ÷ d + e = ( - 6 ) × ( - 1.5 ^ { 2 } ) - ( - 2 ) ÷ \frac { 3 } { 4 } - \frac { 2 } { 3 } = ( - 6 ) × \left( - \frac { 9 } { 4 } \right) + \frac { 8 } { 3 } - \frac { 2 } { 3 } = \frac { 27 } { 2 } + 2 = \frac { 31 } { 2 } $。故选 A。
3. (2025·扬州期末)对于任意四个有理数a,b,c,d.规定:$\begin{vmatrix} a&b\\ c&d\end{vmatrix} = ad-bc$.如:$\begin{vmatrix} 1&2\\ 3&4\end{vmatrix} = 1×4-2×3= -2$.
根据上述规定解决下列问题:
(1)求$\begin{vmatrix} 5&-4\\ 3&2\end{vmatrix} $的值;
(2)若$\begin{vmatrix} -3&\frac {1}{2}x+1\\ 2&2x-1\end{vmatrix} = 15$,求x;
(3)若$\begin{vmatrix} k&x+1\\ 2&3x-1\end{vmatrix} $的值与x的取值无关,求k的值.
答案:3. (1) 因为 $ \left| \begin{array} { l l } { a } & { b } \\ { c } & { d } \end{array} \right| = a d - b c $,所以 $ \left| \begin{array} { c c } { 5 } & { - 4 } \\ { 3 } & { 2 } \end{array} \right| = 5 × 2 - ( - 4 ) × 3 = 10 + 12 = 22 $。
(2) 因为 $ \left| \begin{array} { c c } { - 3 } & { \frac { 1 } { 2 } x + 1 } \\ { 2 } & { 2 x - 1 } \end{array} \right| = 15 $,所以 $ - 3 × ( 2 x - 1 ) - 2 × \left( \frac { 1 } { 2 } x + 1 \right) = 15 $,$ - 6 x + 3 - x - 2 = 15 $,$ - 6 x - x = 15 - 3 + 2 $,$ - 7 x = 14 $,解得 $ x = - 2 $。
(3) $ \left| \begin{array} { c c } { k } & { x + 1 } \\ { 2 } & { 3 x - 1 } \end{array} \right| = k ( 3 x - 1 ) - 2 ( x + 1 ) = 3 k x - k - 2 x - 2 = ( 3 k - 2 ) x - k - 2 $。因为 $ \left| \begin{array} { c c } { k } & { x + 1 } \\ { 2 } & { 3 x - 1 } \end{array} \right| $的值与 $ x $的取值无关,所以 $ 3 k - 2 = 0 $,所以 $ k = \frac { 2 } { 3 } $。
4. (2025·宿迁期末)定义:关于x的方程$ax-b= 0与bx-a= 0$(a,b均为不等于0的常数)称互为“反对方程”.
例如:方程$2x-1= 0与x-2= 0$互为“反对方程”;方程$3x-2= 2x+3$,通过转化可得$x-5= 0$,所以$3x-2= 2x+3与5x-1= 0$互为“反对方程”.
(1)若关于x的方程$3x-2= 0与2x-a= 0$(a为不等于0的常数)互为“反对方程”,则$a= $
3
;
(2)若关于x的方程$5x-b= 2$(b为不等于0的常数)的解为$x= 3$,求b的值及它的“反对方程”的解;
因为关于x的方程5x - b = 2的解为x = 3,所以5×3 - b = 2,解得b = 13。原方程可转化为5x - 15 = 0,其“反对方程”为15x - 5 = 0,解15x - 5 = 0得x = 1/3。
(3)若关于x的方程$\frac {1}{2025}x-c= -x+5$(c为不等于0的常数)的解为$x= 2025$,请直接写出$(c+5)x-\frac {1}{2025}= 1$的解.
x = 1/2025
答案:4. (1) 3 解析:由题可知 $ a x - b = 0 $与 $ b x - a = 0 $($ a $,$ b $均为不等于 0 的常数)称互为“反对方程”,因为 $ 3 x - 2 = 0 $与方程 $ 2 x - a = 0 $互为“反对方程”,所以 $ a = 3 $。
(2) 因为关于 $ x $的方程 $ 5 x - b = 2 $($ b $为不等于 0 的常数)的解为 $ x = 3 $,所以 $ 5 × 3 - b = 2 $,所以 $ b = 13 $,所以 $ 5 x - 13 = 2 $,所以 $ 5 x - 15 = 0 $,所以关于 $ x $的方程 $ 5 x - 15 = 0 $的“反对方程”为 $ 15 x - 5 = 0 $,所以 $ x = \frac { 1 } { 3 } $。
(3) $ x = \frac { 1 } { 2025 } $ 解析:因为关于 $ x $的方程 $ a x - b = 0 $的解为 $ x = \frac { b } { a } $,关于 $ x $的方程 $ b x - a = 0 $的解为 $ x = \frac { a } { b } $,且关于 $ x $的方程 $ a x - b = 0 $与 $ b x - a = 0 $($ a $,$ b $均为不等于 0 的常数)称互为“反对方程”,所以互为“反对方程”的两个方程的解互为倒数。因为方程 $ \frac { 1 } { 2025 } x - c = - x + 5 $,$ \frac { 1 } { 2025 } x + x - c - 5 = 0 $,所以 $ \left( \frac { 1 } { 2025 } + 1 \right) x - ( c + 5 ) = 0 $。因为方程 $ ( c + 5 ) x - \frac { 1 } { 2025 } = 1 $,所以 $ ( c + 5 ) x - \left( \frac { 1 } { 2025 } + 1 \right) = 0 $,所以方程 $ \frac { 1 } { 2025 } x - c = - x + 5 $和方程 $ ( c + 5 ) x - \frac { 1 } { 2025 } = 1 $互为“反对方程”。因为关于 $ x $的方程 $ \frac { 1 } { 2025 } x - c = - x + 5 $($ c $为不等于 0 的常数)的解为 $ x = 2025 $,所以 $ ( c + 5 ) x - \frac { 1 } { 2025 } = 1 $的解为 $ x = \frac { 1 } { 2025 } $。