2025年学霸题中题七年级数学上册苏科版第180页解析答案

3. 如图,将两块直角三角板按如图①放置,$∠ACB= ∠EDF= 90^{\circ },∠ABC= 45^{\circ },∠DFE= 30^{\circ }$,此时点A与点E重合,点A,C,F三点共线.
(1)固定$△ABC$的位置不变,将$△DEF$绕点E按顺时针方向进行旋转,旋转至DE与BC首次平行,如图②所示,此时$∠FAC$的度数是____.
(2)若直线$MN// PQ$,固定$△ABC$的位置不变,将图①中的$△DEF$沿AC方向平移,使得点F正好落在直线MN上,再将$△DEF$绕点F按顺时针方向进行旋转,如图③所示.
①若边EF与边BC交于点G,试判断$∠BGF-∠EFN$的值是否为定值,若是定值,则求出该定值;若不是定值,请说明理由.
②固定$△ABC$的位置不变,将$△DEF$绕点F按顺时针方向以每秒$8^{\circ }$的速度进行旋转,当EF与直线MN首次重合时停止运动,当经过t秒时,线段DE与$△ABC$的一条边平行,请直接写出满足条件的t的值.

答案：
3. (1) $30^{\circ}$ 解析: 因为 $DE // BC$, 所以 $\angle CED = \angle BCA = 90^{\circ}$, 所以 $\angle FAC = \angle CED - \angle FAD = 90^{\circ} - 60^{\circ} = 30^{\circ}$.
(2) 是定值, 理由如下: ① 如图①, 过点 $G$ 作直线 $HL // MN$, 则 $HL // PQ$, 所以 $\angle HGF = \angle EFN$, $\angle BGH = \angle ABC$, 所以 $\angle BGF = \angle HGF + \angle BGH = \angle EFN + \angle ABC$, 所以 $\angle BGF - \angle EFN = \angle ABC = 45^{\circ}$.
　　　　

② $t$ 的值为 $\frac{15}{4}$ 或 $\frac{75}{8}$ 或 15. 解析: 共分三种情况:
情况 1: 如图②, $DE // BC$ 时, $\angle DFE = 30^{\circ}$, 所以 $8t = 30$, 所以 $t = \frac{15}{4}$.
情况 2: 如图③, $DE // AB$ 时, 设 $DF$ 与 $PQ$ 交于点 $R$, 所以 $\angle D = \angle PRF = \angle ARF = 90^{\circ}$, 所以 $\angle AFR = 45^{\circ}$, 则旋转了 $75^{\circ}$, 所以 $8t = 75$, 所以 $t = \frac{75}{8}$.
　　

情况 3: 如图④, $DE // AC$ 时, $\angle D = \angle AFD = 90^{\circ}$, 所以 $\angle AFE = 120^{\circ}$, 即旋转了 $120^{\circ}$, 所以 $8t = 120$, 所以 $t = 15$. 综上, $t = \frac{15}{4}$ 或 $\frac{75}{8}$ 或 15.

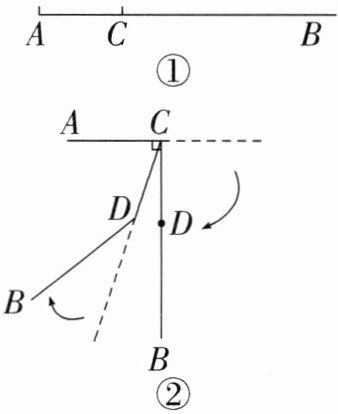
4. (2024·南京期末)如图①,射线AB上有一点C,$AC= 12$,一动点P从点C出发,以每秒m个单位的速度沿射线CB的方向运动,同时,射线CB开始绕点C按顺时针方向以每秒$30^{\circ }$的速度旋转一周.
(1)当CB第一次转至与AC垂直时,$PC= $____;(用含m的代数式表示)
(2)当A,P,C三点中有一个点是另外两个点构成的线段的中点时,求m的值;
(3)如图②,当射线CB绕点C旋转到$CB⊥AC$时,点P到达射线CB上的点D处.此时,射线DB开始绕点D按顺时针方向以每秒$45^{\circ }$的速度一同旋转,旋转一周停止运动,再经过____s,AC与DB所在直线垂直.

答案：
4. (1) $3m$ 解析: 由题意知, 当 $CB$ 第一次转至与 $AC$ 垂直, 即旋转角为 $90^{\circ}$, 所以时间为 $\frac{90^{\circ}}{30^{\circ}} = 3(\mathrm{~s})$, 所以 $PC = 3m$.
(2) 由题意知, 当 $CB$ 绕点 $C$ 顺时针旋转 $180^{\circ}$ 时, 时间为 $\frac{180^{\circ}}{30^{\circ}} = 6(\mathrm{~s})$, 当 $A, P, C$ 三点中有一个点是另外两个点构成的线段的中点时,
① 当 $P$ 为 $AC$ 的中点时, $PC = \frac{1}{2}AC$, 即 $6m = \frac{1}{2} × 12 = 6$, 解得 $m = 1$;
② 当 $A$ 为 $PC$ 的中点时, $PC = 2AC$, 即 $6m = 2 × 12 = 24$, 解得 $m = 4$; 当 $CB$ 绕点 $C$ 顺时针旋转 $360^{\circ}$ 时, 时间为 $\frac{360^{\circ}}{30^{\circ}} = 12(\mathrm{~s})$, 当 $C$ 为 $AP$ 的中点时, $PC = AC$, 即 $12m = 12$, 解得 $m = 1$.
综上, $m$ 的值为 1 或 4.
(3) $\frac{12}{5}$ 或 $\frac{24}{5}$ 或 $\frac{36}{5}$ 解析: 设再经过时间为 $t \mathrm{~s}$, $CD$ 在射线 $CF$ 上, $CE$ 垂直于 $AC$, 由题意知, 分三种情况求解:
情况一: 如图①,
　

此时 $\angle DCE = 30t^{\circ}$, $\angle BDF = 45t^{\circ}$, 所以 $\angle ACD = 90^{\circ} - 30t^{\circ}$, $\angle BDC = 180^{\circ} - 45t^{\circ}$. 因为 $AC$ 与 $DB$ 所在直线垂直, 所以 $\angle BDC + \angle ACD = 90^{\circ}$, 即 $180^{\circ} - 45t^{\circ} + 90^{\circ} - 30t^{\circ} = 90^{\circ}$, 解得 $t = \frac{12}{5}$;
情况二: 如图②,
此时 $\angle DCE = 30t^{\circ}$, $\angle BDC = 45t^{\circ} - 180^{\circ}$, 所以 $\angle ACD = 30t^{\circ} - 90^{\circ}$. 因为 $AC$ 与 $DB$ 所在直线垂直, 所以 $\angle BDC + \angle ACD = 90^{\circ}$, 即 $45t^{\circ} - 180^{\circ} + 30t^{\circ} - 90^{\circ} = 90^{\circ}$, 解得 $t = \frac{24}{5}$;
情况三: 如图③, 射线 $DB$ 的延长线交直线 $AC$ 于点 $H$,
此时 $\angle DCE = 360^{\circ} - 30t^{\circ}$, $\angle BDC = 45t^{\circ} - 180^{\circ}$, 所以 $\angle DCH = 270^{\circ} - 30t^{\circ}$, $\angle CDH = 360^{\circ} - 45t^{\circ}$. 因为 $AC$ 与 $DB$ 所在直线垂直, 所以 $\angle CDH + \angle DCH = 90^{\circ}$, 即 $360^{\circ} - 45t^{\circ} + 270^{\circ} - 30t^{\circ} = 90^{\circ}$, 解得 $t = \frac{36}{5}$.
综上所述, 再经过 $\frac{12}{5} \mathrm{~s}$ 或 $\frac{24}{5} \mathrm{~s}$ 或 $\frac{36}{5} \mathrm{~s}$, $AC$ 与 $DB$ 所在直线垂直, 故答案为 $\frac{12}{5}$ 或 $\frac{24}{5}$ 或 $\frac{36}{5}$.