2. 新考法 (2024·镇江期末)游乐园的摩天轮深受学生们的喜爱,如图是某游乐园的摩天轮的平面示意图,16个座舱均匀分布在圆形转轮边缘,摩天轮以固定的速度绕中心逆时针方向转动,转一周需要30min.座舱与圆形转轮边缘的连接点按顺时针依次标注为$M_{i}(i= 1,2... ... 16),△AOB$表示的是摩天轮的支架,且$∠AOB= 60^{\circ }.$
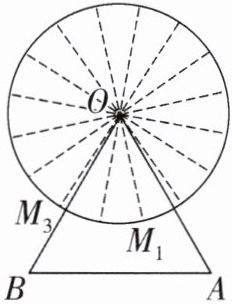
(1)摩天轮每分钟转动____$^{\circ },∠M_{1}OM_{3}= $____$^{\circ }.$
(2)如图,在某一时刻,连接点$M_{1}转动到∠AOB$的内部,此时$∠AOM_{1}= 18^{\circ }$,以此时刻为初始时刻.
①求此时的$∠BOM_{3}$的度数.
②求当$OM_{3}$第一次平分$∠AOB$时,摩天轮的转动时间以及此时$∠AOM_{1}$的度数.
③设摩天轮转动的时间为$t(min)$,在连接点$M_{1}$第一次到达最高处前,是否存在$∠BOM_{3}= 2∠AOM_{1}$的时刻?若存在,求出t的值,若不存在,请说明理由.
[答案]:2. (1)
12
45
解析: 摩天轮每分钟转动的角度是 $360^{\circ} ÷ 30 = 12^{\circ}$, $\angle M_{1}OM_{3} = \frac{2}{16} × 360^{\circ} = 45^{\circ}$.
(2) ① 因为 $\angle AOB = 60^{\circ}$, $\angle AOM_{1} = 18^{\circ}$, 所以 $\angle BOM_{1} = \angle AOB - \angle AOM_{1} = 60^{\circ} - 18^{\circ} = 42^{\circ}$. 又因为 $\angle M_{1}OM_{3} = 45^{\circ}$, 所以 $\angle BOM_{3} = \angle M_{1}OM_{3} - \angle BOM_{1} = 45^{\circ} - 42^{\circ} = 3^{\circ}$.
② 作 $\angle AOB$ 的平分线 $OC$ 交 $AB$ 于点 $C$, 则 $\angle BOC = \frac{1}{2}\angle AOB = \frac{1}{2} × 60^{\circ} = 30^{\circ}$, $OM_{3}$ 第一次平分 $\angle AOB$ 时, $OM_{3}$ 转动了 $30^{\circ} + 3^{\circ} = 33^{\circ}$, 所以转动时间为 $\frac{33}{12} = \frac{11}{4}(\mathrm{~min})$, $OM_{1}$ 转动的角度也是 $33^{\circ}$, 所以此时 $\angle AOM_{1} = 33^{\circ} - 18^{\circ} = 15^{\circ}$.
③ 存在, $t$ 的值为
$\frac{11}{4}$
或
$\frac{13}{12}$
. 理由如下:
因为 $OC$ 是 $\angle AOB$ 的平分线, 所以 $\angle AOC = \angle BOC = 30^{\circ}$. 初始时刻, $\angle COM_{1} = \angle AOC - \angle AOM_{1} = 30^{\circ} - 18^{\circ} = 12^{\circ}$, 当点 $M_{1}$ 第一次到达最高处时, 时间为 $\frac{180 - 12}{12} = 14(\mathrm{~min})$, 所以 $0 < t < 14$ 或 $t = 0$ 或 $t = 14$. 根据题意得 $\angle BOM_{3} = |3 - \angle BOM_{3} = |3 - 12t|^{\circ}$, $\angle AOM_{1} = |18 - 12t|^{\circ}$, $\angle AOM_{1} = |18 - 12t|^{\circ}$, 因为 $\angle BOM_{3} = 2 \angle AOM_{1}$, 即 $|3 - 12t| = 2|18 - 12t|$, 解得 $t = \frac{11}{4}$ 或 $\frac{13}{12}$, 所以存在, $t$ 的值为 $\frac{11}{4}$ 或 $\frac{13}{12}$.
易错提醒
① 注意射线旋转的起始位置, 并留意旋转的方向和速度; ② 注意运动的时间有没有范围限制, 先明确运动的时间范围, 当超出范围时要舍去答案; ③ 注意分类讨论, 找出所有的可能; ④ 当表示的角度不能确定时考虑使用绝对值, 再利用绝对值进行分类计算.