1. (2024·无锡期末)已知有公共端点的射线OA,OB,OC,OD,若点$P_{1},P_{2},P_{3},... $,按如图所示规律排列,则点$P_{2024}$落在 (
C
)
A.射线OA上
B.射线OB上
C.射线OC上
D.射线OD上
答案:C解析:由题图可得,$P_{1}$到$P_{5}$顺时针,$P_{5}$到$P_{9}$逆时针,每8个点为一个周期循环,因为$(2024 - 1)÷8 = 252\cdots\cdots7$,所以点$P_{2024}$落在射线$OC$上.故选C.
2. (2024·常州期末)如图,正方形的边长均是a,以图①,②,③呈现的规律类推,图⑩中所有圆的周长的和是 (
C
)
A.πa
B.5πa
C.10πa
D.20πa
答案:C 解析:题图①中所有圆的周长和:$\pi a$,
题图②中所有圆的周长和:$\frac{1}{2}\pi a\cdot4=\frac{1}{2}\pi a\cdot2^{2}=2\pi a$,
题图③中所有圆的周长和:$\frac{1}{3}\pi a\cdot9=\frac{1}{3}\pi a\cdot3^{2}=3\pi a$,
……
则题图ⓝ中所有圆的周长和:$\frac{1}{n}\pi a\cdot n^{2}=n\pi a$,
则图⑩中所有圆的周长和为$10\pi a$,故选C.
3. (2025·盐城期末)如图①所示的是中国南宋数学家杨辉在《九章算法》中出现的三角形状的数列,又称为“杨辉三角形”,该三角形中的数据排列有着一定的规律,若将其中一组斜数列用字母$a_{1},a_{2},a_{3}... ... $代替,如图②,则$a_{59}+a_{60}$的值为 (
C
)
A.3 580
B.3 590
C.3 600
D.3 720
答案:C 解析:$a_{1}=1,a_{2}=1 + 2 = 3,a_{3}=1 + 2 + 3 = 6,a_{4}=1 + 2 + 3 + 4 = 10,a_{5}=1 + 2 + 3 + 4 + 5 = 15,\cdots$;则$a_{n}=1 + 2 + 3 + \cdots + n=\frac{n(1 + n)}{2}$,所以$a_{59}+a_{60}=\frac{59×(59 + 1)}{2}+\frac{60×(60 + 1)}{2}=1770 + 1830 = 3600$.故选C.
4. 已知数$a= 1^{5}+2^{5}+3^{5}+4^{5}+5^{5}+... +29^{5}$,这个数a的个位数为 (
C
)
A.3
B.4
C.5
D.6
答案:C 解析:因为$1^{5}$的个位数是$1,2^{5}$的个位数是$2,3^{5}$的个位数是$3,4^{5}$的个位数是$4,5^{5}$的个位数是$5,6^{5}$的个位数是$6,7^{5}$的个位数是$7,8^{5}$的个位数是$8,9^{5}$的个位数是$9,10^{5}$的个位数是$0$,由此可发现$n^{5}$的个位数与$n$的个位数相同,所以$a$的个位数应是$1 + 2 + 3 + \cdots + 9 + 0 + 1 + 2 + 3 + \cdots + 9 + 0 + 1 + 2 + 3 + \cdots + 9$的结果的个位数,且该结果的个位数是5.故选C.
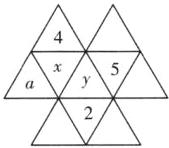
5. 在如图所示的图案中,每个小三角形的边长都为1,把由四个小三角形组成的边长为2的大三角形称为一个“单元”,现将1,2,3,4,5,6,7,8,9,10这十个数分别填入图中的十个小三角形中,使得对于图中的四个“单元”,每个“单元”中的四个数之和都是23,若2,4,5,a已填入图中,位置如图所示,则a表示的数是____.
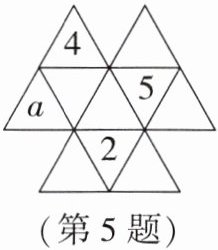
答案:3 解析:如图,由题意得$x + y + 2 + 5 = 23$,所以$x + y = 16$.又因为$4 + a + x + y = 23$,即$4 + a + 16 = 23$,所以$a = 3$.
6. (2025·盐城期末)如图,甲、乙两动点分别从正八边形ABCDEFGH的顶点A,G同时出发,沿正八边形的边移动.甲点依顺时针环形运动,乙点依逆时针环形运动.若乙的速度是甲的速度的3倍,则它们第2025次相遇在正八边形的边
AH
上.(用字母表示)
答案:$AH$解析:设正八边形的边长为$a$,甲的速度为$v$,则乙的速度为$3v$,根据题意,得第一次相遇甲、乙走的总路程为$2a$,则第一次相遇的用时为$\frac{2a}{v + 3v}=\frac{a}{2v}$,此时甲走了$\frac{a}{2v}× v=\frac{1}{2}a$,即相遇在正八边形的边$AH$上;第二次相遇甲、乙走的总路程为$8a$,则第二次相遇的用时为$\frac{8a}{v + 3v}=\frac{2a}{v}$,此时甲走了$\frac{2a}{v}× v = 2a$,即相遇在正八边形的边$GF$上;第三次相遇甲、乙走的总路程为$8a$,则第三次相遇的用时为$\frac{8a}{v + 3v}=\frac{2a}{v}$,此时甲走了$\frac{2a}{v}× v = 2a$,即相遇在正八边形的边$DE$上;第四次相遇甲、乙走的总路程为$8a$,则第四次相遇的用时为$\frac{8a}{v + 3v}=\frac{2a}{v}$,此时甲走了$\frac{2a}{v}× v = 2a$,即相遇在正八边形的边$BC$上;第五次相遇甲、乙走的总路程为$8a$,则第五次相遇的用时为$\frac{8a}{v + 3v}=\frac{2a}{v}$,此时甲走了$\frac{2a}{v}× v = 2a$,即相遇在正八边形的边$AH$上;依此类推,第五次和第一次相同,所以相遇位置每四次一循环,因为$2025÷4 = 506\cdots\cdots1$,所以第2025次相遇与第一次相同,在正八边形的边$AH$上.
解析:
解:设正八边形边长为$a$,甲速度为$v$,则乙速度为$3v$。
第一次相遇:总路程$2a$,用时$\frac{2a}{v + 3v}=\frac{a}{2v}$,甲走$\frac{a}{2v}×v=\frac{1}{2}a$,相遇在边$AH$。
第二次相遇:总路程$8a$,用时$\frac{8a}{4v}=2\frac{a}{v}$,甲走$2\frac{a}{v}×v = 2a$,相遇在边$GF$。
第三次相遇:总路程$8a$,甲走$2a$,相遇在边$DE$。
第四次相遇:总路程$8a$,甲走$2a$,相遇在边$BC$。
第五次相遇:总路程$8a$,甲走$2a$,相遇在边$AH$,周期为$4$。
$2025÷4 = 506\cdots\cdots1$,第$2025$次与第一次相同,在边$AH$。
答案:$AH$
7. 如图,点M在线段AN的延长线上,且线段$MN= 20$,第一次操作:分别取线段AM和AN的中点$M_{1},N_{1}$;第二次操作:分别取线段$AM_{1}和AN_{1}的中点M_{2},N_{2}$;第三次操作:分别取线段$AM_{2}和AN_{2}的中点M_{3},N_{3}$……连续这样操作10次,则$M_{10}N_{10}= $____
$\frac{5}{2^{8}}$
.
答案:$\frac{5}{2^{8}}$解析:因为线段$MN = 20,M_{1},N_{1}$是线段$AM$和$AN$的中点,所以$M_{1}N_{1}=AM_{1}-AN_{1}=\frac{1}{2}AM-\frac{1}{2}AN=\frac{1}{2}(AM - AN)=\frac{1}{2}MN=\frac{1}{2}×20 = 10$.因为$M_{2},N_{2}$是线段$AM_{1}$和$AN_{1}$的中点,所以$M_{2}N_{2}=AM_{2}-AN_{2}=\frac{1}{2}AM_{1}-\frac{1}{2}AN_{1}=\frac{1}{2}(AM_{1}-AN_{1})=\frac{1}{2}M_{1}N_{1}=\frac{1}{2}×\frac{1}{2}×20 = 5$.发现规律:$M_{n}N_{n}=\frac{1}{2^{n}}×20$,所以$M_{10}N_{10}=\frac{1}{2^{10}}×20=\frac{2×2×5}{2×2×2×2×2×2×2×2×2×2}=\frac{5}{2^{8}}$.
解析:
解:因为线段$MN = 20$,$M_{1},N_{1}$是线段$AM$和$AN$的中点,所以$M_{1}N_{1}=AM_{1}-AN_{1}=\frac{1}{2}AM - \frac{1}{2}AN=\frac{1}{2}(AM - AN)=\frac{1}{2}MN=\frac{1}{2}×20 = 10$。
因为$M_{2},N_{2}$是线段$AM_{1}$和$AN_{1}$的中点,所以$M_{2}N_{2}=AM_{2}-AN_{2}=\frac{1}{2}AM_{1}-\frac{1}{2}AN_{1}=\frac{1}{2}(AM_{1}-AN_{1})=\frac{1}{2}M_{1}N_{1}=\frac{1}{2}×10 = 5$。
同理可得,$M_{3}N_{3}=\frac{1}{2}M_{2}N_{2}=\frac{1}{2}×5=\frac{5}{2}$,以此类推,规律为$M_{n}N_{n}=\frac{1}{2^{n}}×20$。
则$M_{10}N_{10}=\frac{1}{2^{10}}×20=\frac{20}{1024}=\frac{5}{256}=\frac{5}{2^{8}}$。
$\frac{5}{2^{8}}$
8. (2024·扬州期末)设一列数$|a_{1}|,|a_{2}|,|a_{3}|,...,|a_{2024}|$中任意三个相邻数之和都是20,已知$|a_{6}|= 9,|a_{14}|= 2x,|a_{31}|= x+2$,那么$|a_{2024}-a_{2023}|= $
1或11
.
答案:1或11 解析:因为一列数$|a_{1}|,|a_{2}|,|a_{3}|,\cdots,|a_{2024}|$中任意三个相邻数之和都是20,所以$|a_{3n + 1}| = |a_{1}|,|a_{3n + 2}| = |a_{2}|,|a_{3n + 3}| = |a_{3}|$($n$为自然数).因为$|a_{6}| = 9,|a_{14}| = 2x,|a_{31}| = x + 2$,所以$|a_{1}| = x + 2,|a_{2}| = 2x,|a_{3}| = 9$,所以$x + 2 + 2x + 9 = 20$,所以$x = 3$,所以$|a_{1}| = 5,|a_{2}| = 6$.因为$|a_{2024}| = 6,|a_{2023}| = 5$,所以$a_{2024}=\pm6,a_{2023}=\pm5$,所以$|a_{2024}-a_{2023}| = 1$或11.
解析:
解:因为一列数$|a_{1}|,|a_{2}|,|a_{3}|,\cdots,|a_{2024}|$中任意三个相邻数之和都是20,所以该数列的绝对值部分具有周期性,周期为3,即$|a_{3n + 1}| = |a_{1}|,|a_{3n + 2}| = |a_{2}|,|a_{3n + 3}| = |a_{3}|$($n$为自然数)。
因为$6 = 3×2$,所以$|a_{6}| = |a_{3}| = 9$;$14 = 3×4 + 2$,所以$|a_{14}| = |a_{2}| = 2x$;$31 = 3×10 + 1$,所以$|a_{31}| = |a_{1}| = x + 2$。
由题意得$|a_{1}| + |a_{2}| + |a_{3}| = 20$,即$x + 2 + 2x + 9 = 20$,解得$x = 3$。
所以$|a_{1}| = 3 + 2 = 5$,$|a_{2}| = 2×3 = 6$,$|a_{3}| = 9$。
因为$2024 = 3×674 + 2$,所以$|a_{2024}| = |a_{2}| = 6$;$2023 = 3×674 + 1$,所以$|a_{2023}| = |a_{1}| = 5$。
则$a_{2024} = ±6$,$a_{2023} = ±5$。
当$a_{2024} = 6$,$a_{2023} = 5$时,$|a_{2024} - a_{2023}| = |6 - 5| = 1$;
当$a_{2024} = 6$,$a_{2023} = -5$时,$|a_{2024} - a_{2023}| = |6 - (-5)| = 11$;
当$a_{2024} = -6$,$a_{2023} = 5$时,$|a_{2024} - a_{2023}| = |-6 - 5| = 11$;
当$a_{2024} = -6$,$a_{2023} = -5$时,$|a_{2024} - a_{2023}| = |-6 - (-5)| = 1$。
综上,$|a_{2024} - a_{2023}| = 1$或$11$。
答案:1或11
9. 黑板上写有1,2,3,…,100共100个数,每次操作先从黑板上的数中选取2个数a,b,然后擦去a,b,并在黑板上写$a+b+1$,则经过
99
次操作后,黑板上只剩下一个数,这个数是
5149
.
答案:99 5149解析:每一次擦去都会将被擦去的数相加再加1,$1\sim100$的每一个数最后都会被擦去,总共擦去99次,因此最后留下的数是$1 + 2 + 3 + \cdots + 100 + 99×1 = 5050 + 99 = 5149$.
解析:
解:每次操作减少1个数,最初有100个数,最后剩1个数,所以操作次数为$100-1=99$次。
因为每次操作擦去a,b,写上$a+b+1$,即每次操作后所有数的总和增加1。经过99次操作,总和共增加99。
又因为1到100的和为$\frac{100×(100+1)}{2}=5050$,所以最后剩下的数是$5050+99=5149$。
99;5149