1. 先化简,再求值:
(1)(2025·泰州期末)$\frac {3}{2}y-(\frac {5}{2}y-1)+3(4-y)$,其中$y= -3$.
(2)(2025·盐城期末)$3x^{2}y-2(xy^{2}-3x^{2}y)+4(x^{2}y-2xy^{2})$,其中$x= 2,y= -1$.
(3)(2024·苏州期末)$4xy-[(x^{2}+5xy-y^{2})-(x^{2}+3xy-2y^{2})]$,其中$(x-1)^{2}+|y+\frac {1}{2}|= 0$.
答案:(1) 原式$=\frac{3y}{2}-\frac{5y}{2}+1+12-3y=-4y+13$,当$y=-3$时,原式$=-4y+13=-4×(-3)+13=25$。(2) 原式$=3x^{2}y-2xy^{2}+6x^{2}y+4x^{2}y-8xy^{2}=13x^{2}y-10xy^{2}$。当$x=2$,$y=-1$时,原式$=13x^{2}y-10xy^{2}=13×2^{2}×(-1)-10×2×(-1)^{2}=13×4×(-1)-10×2×1=-52-20=-72$。(3) 原式$=4xy-(x^{2}+5xy-y^{2}-x^{2}-3xy+2y^{2})=4xy-(2xy+y^{2})=4xy-2xy-y^{2}=2xy-y^{2}$。因为$(x - 1)^{2}+\left|y+\frac{1}{2}\right|=0$,所以$x = 1$,$y=-\frac{1}{2}$,代入得原式$=-\frac{5}{4}$。
2. (2024·南京校级期末)若化简代数式$(x^{3}+bx^{2}-1)-(2ax^{3}-x^{2}+x)的结果中不含x^{2}和x^{3}$项.
(1)试求$a,b$的值;
(2)在(1)的条件下,先化简,再求值:$2(a^{2}-ab+1)-3(\frac {2}{3}a^{2}-2ab+4)$.
答案:(1) 原式$=x^{3}+bx^{2}-1-2ax^{3}+x^{2}-x=(1 - 2a)x^{3}+(b + 1)x^{2}-x - 1$,由题意得$1 - 2a = 0$且$b + 1 = 0$,解得$a=\frac{1}{2}$,$b=-1$。(2) 原式$=2a^{2}-2ab+2-2a^{2}+6ab-12=4ab-10$,当$a=\frac{1}{2}$,$b=-1$时,原式$=4×\frac{1}{2}×(-1)-10=-12$。
3. (2025·南京期末)将四张正方形纸片①,②,③,
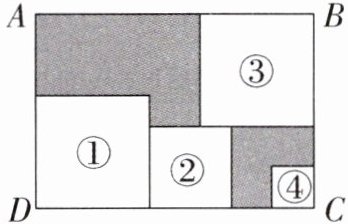
④按如图方式放入长方形$ABCD$内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示,要求出图中两块阴影部分的周长之差,只需知道其中一个正方形的边长即可,则要知道的那个正方形编号是( )
A.①
B.②
C.③
D.④
答案:A 解析:设正方形纸片①,②,③,④的边长分别为$a$,$b$,$c$,$d$,如图,左上角阴影部分的周长为$2(AB - c + AD - b)$,右下角阴影部分的周长为$2(AB - a - b + AD - c)$,所以两块阴影部分周长之差为$2(AB - c + AD - b)-2(AB - a - b + AD - c)=2AB - 2c + 2AD - 2b - 2AB + 2a + 2b - 2AD + 2c = 2a$,所以要求出图中两块阴影部分的周长之差,只需知道正方形①的边长即可,故选A。

4. (2025·徐州期末)综合与探究:
某新建的交通环岛的简化模型如图,试通车前环岛上没有车辆,试通车期间进出该交通环岛的机动车数量如图所示,箭头方向表示车辆的行驶方向,路口的整式表示驶入或驶出的车辆数,如路口$AH在此期间驶入(a-b)$辆机动车,驶出$2b$辆机动车.图中$x_{1},x_{2},x_{3}分别表示在试通车期间通过路段EH,AB,CD$的所有机动车数量.
(1)若$x_{1}= 10$,则:
①当$a= 3,b= 2$时,求$x_{2},x_{3}$的值;
②用含$a,b的代数式表示x_{2},x_{3}$.
(2)若试通车期间,通过路段$AB,EH$的车辆数相同,且通过路段$CD的车辆比通过路段EH的车辆少10$辆,求$a,b$的值.

答案:(1) ①当$x_{1}=10$时,$x_{2}=x_{1}-2b+(a - b)=10 + a - 3b$,$x_{3}=x_{2}-(a + b)+2b=10 + a - 3b-(a + b)+2b=10 - 2b$,当$a = 3$,$b = 2$时:$x_{2}=10 + a - 3b=10 + 3 - 3×2=7$;$x_{3}=10 - 2b=10 - 2×2=6$。②由①知$x_{2}=10 + a - 3b$,$x_{3}=10 - 2b$。(2) 通过路段$AB$的车辆数为$x_{2}=x_{1}+a - 3b$,通过路段$EH$的车辆数为$x_{1}$,通过路段$CD$的车辆数为$x_{3}=x_{1}-2b$,因为通过路段$AB$,$EH$的车辆数相同,所以$x_{1}+a - 3b=x_{1}$,所以$a - 3b = 0$。因为通过路段$CD$的车辆比通过路段$EH$的车辆少$10$辆,所以$x_{1}-x_{3}=x_{1}-(x_{1}-2b)=10$,所以$b = 5$,把$b = 5$代入$a - 3b = 0$,得$a - 15 = 0$,所以$a = 15$。综上,$a = 15$,$b = 5$。
解析:
(1) ①解:当$x_{1}=10$,$a=3$,$b=2$时,
$x_{2}=x_{1}+a - 3b=10 + 3 - 3×2=7$
$x_{3}=10 - 2b=10 - 2×2=6$
②解:$x_{2}=10 + a - 3b$,$x_{3}=10 - 2b$
(2) 解:由题意得$\begin{cases}x_{1}+a - 3b=x_{1}\\x_{1}-(x_{1}-2b)=10\end{cases}$
解得$\begin{cases}a - 3b=0\\2b=10\end{cases}$
$\therefore b=5$,$a=15$
综上,$a=15$,$b=5$