答案：
(1) $ -12 $; $ 8 - 5t $ (2) 若点 $ P $, $ Q $ 同时出发,设 $ t $ 秒时 $ P $, $ Q $ 之间的距离恰好等于 2. 根据题意,得 $ 3t + 5t = 20 - 2 $ 或 $ 3t + 5t = 20 + 2 $,解得 $ t = \frac{9}{4} $ 或 $ t = \frac{11}{4} $. 即若点 $ P $, $ Q $ 同时出发, $ \frac{9}{4} $ 秒或 $ \frac{11}{4} $ 秒时, $ P $, $ Q $ 之间的距离恰好等于 2. (3) 设点 $ P $ 运动 $ t $ 秒时追上点 $ Q $,根据题意,得 $ 5t - 3t = 20 $,解得 $ t = 10 $. 即若点 $ P $, $ Q $ 同时出发,点 $ P $ 运动 10 秒时追上点 $ Q $. (4) 线段 $ MN $ 的长度不发生变化,都等于 10. ① 当点 $ P $ 在 $ A $, $ B $ 两点之间运动时,如图①. 　　　　　　　 $ MN = MP + NP = \frac{1}{2} AP + \frac{1}{2} BP = \frac{1}{2} ( AP + BP ) = \frac{1}{2} AB = \frac{1}{2} × 20 = 10 $. ② 当点 $ P $ 运动到点 $ B $ 的左侧时,如图②. 　　　　　 $ MN = MP - NP = \frac{1}{2} AP - \frac{1}{2} BP = \frac{1}{2} ( AP - BP ) = \frac{1}{2} AB = \frac{1}{2} × 20 = 10 $. 综上,线段 $ MN $ 的长度不发生变化,其值为 10.

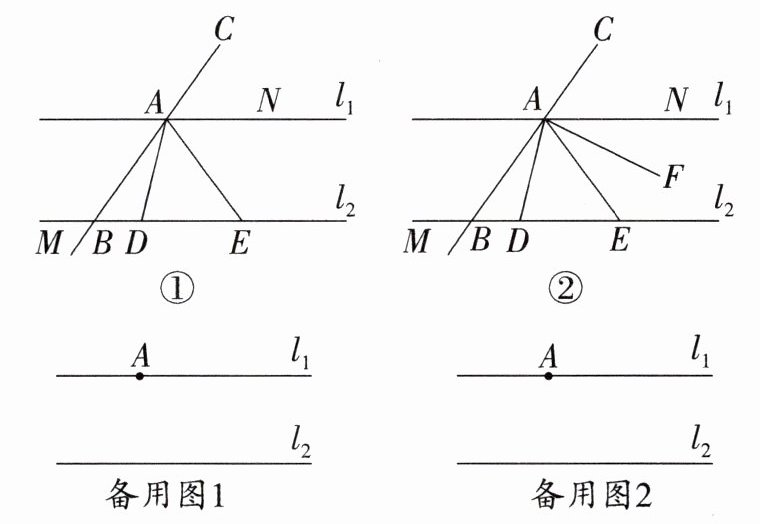
答案：
(1) 125 解析:如图①所示,因为 $ l_1 // l_2 $,所以 $ \angle ABM = \angle BAN $, $ \angle NAE = \angle AED = 50^{\circ} $.因为 $ \angle BAD = 25^{\circ} $, $ \angle DAE = \angle AED = 50^{\circ} $,所以 $ \angle ABM = \angle BAN = \angle BAD + \angle DAE + \angle NAE = 25^{\circ} + 50^{\circ} + 50^{\circ} = 125^{\circ} $. (2) ① $ \angle ABD = 2 \angle EAF $. 理由:因为 $ l_1 // l_2 $,所以 $ \angle CAN = \angle ABD $, $ \angle NAE = \angle AED $. 又因为 $ AF $ 平分 $ \angle CAD $,所以 $ \angle DAF = \angle CAF = \frac{1}{2} \angle CAD $. 因为 $ \angle DAE = \angle AED = \angle NAE $,所以 $ \angle DAE = \frac{1}{2} ( \angle DAE + \angle NAE ) = \frac{1}{2} \angle DAN $,所以 $ \angle EAF = \angle DAF - \angle DAE = \frac{1}{2} \angle CAD - \frac{1}{2} \angle DAN = \frac{1}{2} \angle CAN = \frac{1}{2} \angle ABD $. 即 $ \angle ABD = 2 \angle EAF $. 　　 　　 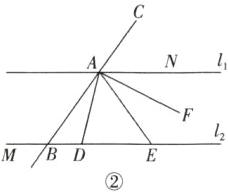② $ 30^{\circ} $ 或 $ 110^{\circ} $ 解析:Ⅰ. 如图②所示,点 $ D $ 在点 $ B $ 右侧,此时有 $ \angle EAF = \frac{1}{2} \angle ABD $,因为 $ \angle ABM + \angle EAF = 150^{\circ} $,所以 $ \angle ABM + \frac{1}{2} \angle ABD = 150^{\circ} $. 又因为 $ \angle ABM + \angle ABD = 180^{\circ} $,所以 $ \frac{1}{2} \angle ABD = 180^{\circ} - 150^{\circ} = 30^{\circ} $,所以 $ \angle EAF = 30^{\circ} $. Ⅱ. 如图③所示,点 $ D $ 在点 $ B $ 左侧,点 $ E $ 在点 $ B $ 右侧,因为 $ AF $ 平分 $ \angle CAD $,所以 $ \angle DAF = \frac{1}{2} \angle CAD $. 因为 $ l_1 // l_2 $,所以 $ \angle AED = \angle NAE $, $ \angle CAN = \angle ABE $. 因为 $ \angle DAE = \angle AED = \angle NAE $,所以 $ \angle DAE = \frac{1}{2} ( \angle DAE + \angle NAE ) = \frac{1}{2} \angle DAN $,所以 $ \angle EAF = \angle DAF + \angle DAE = \frac{1}{2} ( \angle CAD + \angle DAN ) = \frac{1}{2} × ( 360^{\circ} - \angle CAN ) = 180^{\circ} - \frac{1}{2} \angle ABE $. 因为 $ \angle ABE + \angle ABM = 180^{\circ} $,所以 $ \angle EAF = 180^{\circ} - \frac{1}{2} ( 180^{\circ} - \angle ABM ) = 90^{\circ} + \frac{1}{2} \angle ABM $. 又因为 $ \angle EAF + \angle ABM = 150^{\circ} $,所以 $ \angle EAF = 90^{\circ} + \frac{1}{2} ( 150^{\circ} - \angle EAF ) = 165^{\circ} - \frac{1}{2} \angle EAF $,所以 $ \angle EAF = 110^{\circ} $. Ⅲ. 如图④所示, $ D $, $ E $ 均在点 $ B $ 左侧,此时 $ \angle DAE = \frac{1}{2} \angle DAN $, $ \angle DAF = \frac{1}{2} \angle CAD $, $ \angle EAF = \angle DAE + \angle DAF = \frac{1}{2} ( 360^{\circ} - \angle CAN ) = 180^{\circ} - \frac{1}{2} \angle ABG = 180^{\circ} - \frac{1}{2} ( 180^{\circ} - \angle ABM ) = 90^{\circ} + \frac{1}{2} \angle ABM $,所以 $ \angle EAF = 110^{\circ} $. 综上所述, $ \angle EAF = 30^{\circ} $ 或 $ \angle EAF = 110^{\circ} $.