11. 如图,已知$∠AOB = 150^{\circ}$,$∠COD = 50^{\circ}$,OM平分$∠AOD$,ON平分$∠BOC$,则$∠MON$的度数为
50
$^{\circ}$.
答案:50 解析:因为 $ \angle BOC = \angle BOD + \angle COD $,所以 $ \angle AOD + \angle BOC = \angle AOD + \angle BOD + \angle COD = \angle AOB + \angle COD = 150^{\circ} + 50^{\circ} = 200^{\circ} $.又因为 $ OM $ 平分 $ \angle AOD $, $ ON $ 平分 $ \angle BOC $,所以 $ \angle MOD + \angle CON = \frac{1}{2} × ( \angle AOD + \angle BOC ) = \frac{1}{2} × 200^{\circ} = 100^{\circ} $.又因为 $ \angle MOD = \angle MON + \angle DON $,所以 $ \angle MOD + \angle CON = \angle MON + \angle DON + \angle CON = \angle MON + \angle COD = 100^{\circ} $,即 $ \angle MON + 50^{\circ} = 100^{\circ} $,所以 $ \angle MON = 100^{\circ} - 50^{\circ} = 50^{\circ} $.
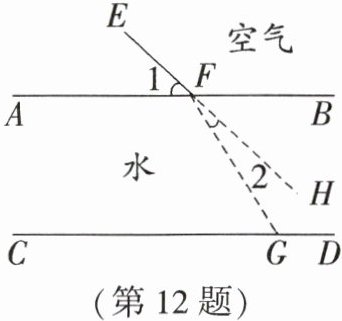
12. (2024·盐城大丰区模拟)光从空气斜射入水中,传播方向会发生变化.如图,表示水面的直线AB与表示水底的直线CD平行,光线EF从空气射入水中,改变方向后射到水底G处,FH是EF的延长线,若$∠1 = 43^{\circ}$,$∠2 = 15^{\circ}$,则$∠CGF$的度数是______.
$58^{\circ}$
答案:$ 58^{\circ} $ 解析:因为 $ \angle 1 = 43^{\circ} $, $ \angle 2 = 15^{\circ} $,所以 $ \angle AFG = 180^{\circ} - \angle 1 - \angle 2 = 180^{\circ} - 43^{\circ} - 15^{\circ} = 122^{\circ} $.因为 $ AB // CD $,所以 $ \angle CGF = 180^{\circ} - \angle AFG = 180^{\circ} - 122^{\circ} = 58^{\circ} $.
13. 如图,把一张长方形的纸条ABCD沿EF折叠,若$∠BFC'比∠BFE多6^{\circ}$,则$∠EFC = $
122
$^{\circ}$.
答案:122 解析:设 $ \angle EFC = x $,则 $ \angle 1 = 180^{\circ} - x $,则 $ \angle BFC' = x - ( 180^{\circ} - x ) = 2x - 180^{\circ} $.因为 $ \angle BFC' $ 比 $ \angle BFE $ 多 $ 6^{\circ} $,所以 $ 2x - 180^{\circ} - ( 180^{\circ} - x ) = 6^{\circ} $,解得 $ x = 122^{\circ} $,即 $ \angle EFC = 122^{\circ} $.
解析:
设$\angle EFC = x$,由平角定义得$\angle 1 = 180^{\circ}-x$。
由折叠性质知$\angle EFC'=\angle EFC = x$,则$\angle BFC'=\angle EFC' - \angle 1=x-(180^{\circ}-x)=2x - 180^{\circ}$。
因为$\angle BFC'$比$\angle BFE$多$6^{\circ}$,且$\angle BFE=\angle 1$,所以$2x - 180^{\circ}-(180^{\circ}-x)=6^{\circ}$。
解得$3x=366^{\circ}$,$x = 122^{\circ}$。
$122$
14. 如图,$∠MAN = 52^{\circ}$,过射线AM上一点C作$CP // AN$,CB平分$∠ACP$,依次作出$∠BCP的平分线CB_1$,$∠B_1CP的平分线CB_2$,$∠B_{n - 1}CP的平分线CB_n$,其中点B,$B_1$,$B_2$,…,$B_{n - 1}$,$B_n$都在射线AN上,若$∠PCB_n = 1^{\circ}$,则$n = $
6
.
答案:6 解析:因为 $ CP // AN $,所以 $ \angle ACP = 180^{\circ} - \angle MAN $.因为 $ CB $ 平分 $ \angle ACP $,所以 $ \angle PCB = \frac{1}{2} \angle ACP = \frac{1}{2} ( 180^{\circ} - \angle MAN ) $.又因为 $ CB_1 $ 平分 $ \angle BCP $,所以 $ \angle PCB_1 = \frac{1}{2} \angle PCB = \frac{1}{2^2} ( 180^{\circ} - \angle MAN ) $,…,所以 $ \angle PCB_n = \frac{1}{2} \angle PCB_{n - 1} = \frac{1}{2^{n + 1}} ( 180^{\circ} - \angle MAN ) $.因为 $ \angle MAN = 52^{\circ} $, $ \angle PCB_n = 1^{\circ} $,所以 $ \frac{1}{2^{n + 1}} ( 180^{\circ} - 52^{\circ} ) = 1^{\circ} $,解得 $ n = 6 $.
解析:
解:因为 $ CP // AN $,所以 $ \angle ACP = 180^{\circ} - \angle MAN $。
因为 $ CB $ 平分 $ \angle ACP $,所以 $ \angle PCB = \frac{1}{2} \angle ACP = \frac{1}{2}(180^{\circ} - \angle MAN) $。
因为 $ CB_1 $ 平分 $ \angle BCP $,所以 $ \angle PCB_1 = \frac{1}{2} \angle PCB = \frac{1}{2^2}(180^{\circ} - \angle MAN) $。
同理可得,$ \angle PCB_n = \frac{1}{2^{n+1}}(180^{\circ} - \angle MAN) $。
因为 $ \angle MAN = 52^{\circ} $,$ \angle PCB_n = 1^{\circ} $,
所以 $ \frac{1}{2^{n+1}}(180^{\circ} - 52^{\circ}) = 1^{\circ} $,
即 $ \frac{128^{\circ}}{2^{n+1}} = 1^{\circ} $,解得 $ 2^{n+1} = 128 $,$ n+1 = 7 $,$ n = 6 $。
答案:$ 6 $
15. (6分)按要求完成下列作图(保留作图痕迹):
如图,在一条笔直的公路两侧,分别有A,B两个村庄.
(1)要在公路l上建一公交站P,使点P到A,B两个村庄距离之和最短,画出点P的位置,理由是______;
(2)在公路上找出一点Q,满足点Q到村庄A距离最近,画出点Q的位置,理由是______.

答案:(1) 如图①,连接 $ AB $ 交直线 $ l $ 于点 $ P $,点 $ P $ 即为所求.两点之间,线段最短


(2) 如图②,过直线 $ l $ 外一点 $ A $ 作 $ l $ 的垂线,垂足为 $ Q $,点 $ Q $ 即为所求.直线外一点与直线上各点连接的所有线段中,垂线段最短
16. (7分)(2024·周口期末)如图,已知F,E分别是射线AB,CD上的点.连接AC,AE平分$∠BAC$,EF平分$∠AED$,$∠2 = ∠3$.
(1)试说明:$AB // CD$;
(2)若$∠AFE - ∠2 = 30^{\circ}$,求$∠AFE$的度数.

答案:(1) 因为 $ AE $ 平分 $ \angle BAC $,所以 $ \angle 1 = \angle 2 $.因为 $ \angle 2 = \angle 3 $,所以 $ \angle 1 = \angle 3 $,所以 $ AB // CD $. (2) 因为 $ \angle AFE - \angle 2 = 30^{\circ} $,所以 $ \angle AFE = \angle 2 + 30^{\circ} $.因为 $ AB // CD $,所以 $ \angle AFE = \angle FED = \angle 2 + 30^{\circ} $.因为 $ EF $ 平分 $ \angle AED $,所以 $ \angle AED = 2 \angle FED = 2 \angle 2 + 60^{\circ} $.因为 $ \angle 3 + \angle AED = 180^{\circ} $,所以 $ \angle 3 + 2 \angle 2 + 60^{\circ} = 180^{\circ} $.因为 $ \angle 3 = \angle 2 $,所以 $ \angle 2 = 40^{\circ} $,所以 $ \angle AFE = \angle 2 + 30^{\circ} = 70^{\circ} $,所以 $ \angle AFE $ 的度数为 $ 70^{\circ} $.
解析:
(1) 因为 AE 平分∠BAC,所以∠1=∠2。因为∠2=∠3,所以∠1=∠3,所以 AB//CD。
(2) 因为∠AFE - ∠2 = 30°,所以∠AFE = ∠2 + 30°。因为 AB//CD,所以∠AFE = ∠FED = ∠2 + 30°。因为 EF 平分∠AED,所以∠AED = 2∠FED = 2∠2 + 60°。因为∠3 + ∠AED = 180°,所以∠3 + 2∠2 + 60° = 180°。因为∠3 = ∠2,所以∠2 = 40°,所以∠AFE = 40° + 30° = 70°。
∠AFE 的度数为 70°。
17. (7分)如图,已知点D是线段AB上一点,点C是线段AB的中点,若$AB = 8cm$,$BD = 3cm$.
(1)求线段CD的长;
(2)若点E是直线AB上一点,且$BE = \frac{1}{3}BD$,点F是BE的中点,求线段CF的长.

答案:(1) 因为点 $ C $ 是线段 $ AB $ 的中点, $ AB = 8 \, \text{cm} $,所以 $ BC = \frac{1}{2} AB = \frac{1}{2} × 8 = 4 \, \text{cm} $,所以 $ CD = BC - BD = 4 - 3 = 1 \, \text{cm} $. (2) ① 当点 $ E $ 在点 $ B $ 的右侧时,如图①.

因为 $ BE = \frac{1}{3} BD $,所以 $ BE = \frac{1}{3} × 3 = 1 \, \text{cm} $.因为点 $ F $ 是 $ BE $ 的中点,所以 $ BF = \frac{1}{2} BE = \frac{1}{2} × 1 = \frac{1}{2} \, \text{cm} $,所以 $ CF = BC + BF = 4 + \frac{1}{2} = 4 \frac{1}{2} \, \text{cm} $. ② 当点 $ E $ 在点 $ B $ 的左侧时,如图②.

因为 $ BE = \frac{1}{3} BD $,所以 $ BE = \frac{1}{3} × 3 = 1 \, \text{cm} $.因为点 $ F $ 是 $ BE $ 的中点,所以 $ BF = \frac{1}{2} BE = \frac{1}{2} × 1 = \frac{1}{2} \, \text{cm} $,所以 $ CF = BC - BF = 4 - \frac{1}{2} = 3 \frac{1}{2} \, \text{cm} $. 综上,线段 $ CF $ 的长为 $ 4 \frac{1}{2} \, \text{cm} $ 或 $ 3 \frac{1}{2} \, \text{cm} $.