1. 如图,平面内三条直线两两相交于 $ A $,$ B $,$ C $ 三点,此时平面被分割成了 $ 7 $ 个不同的区域,点 $ N $ 为平面内三条直线外另一点,若过点 $ N $ 再画一条直线(请在图上画出),使此时平面被分成最多不同区域,则此时最多不同区域的个数为______。

2. (1) 探究一,模型再现：$ m $ 条直线最多可以把平面分割成多少个部分？
如图①,平面中画出 $ 1 $ 条直线时,最多可以把平面分割成 $ 2 $ 个部分；如图②,平面中画出 $ 2 $ 条直线时,最多可以把平面分割成 $ 4 $ 个部分；如图③,平面中画出 $ 3 $ 条直线时,最多可以把平面分割成 $ 7 $ 个部分……

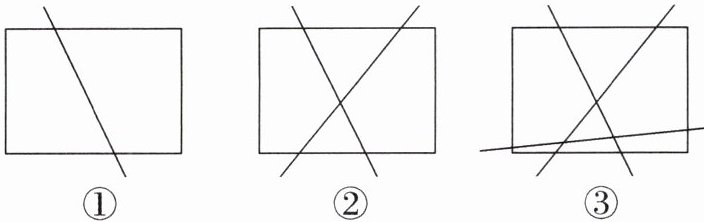
问题一：$ 5 $ 条直线最多可以把平面分割成个部分。
(2) 探究二,类比迁移：$ n $ 个圆最多可以把平面分割成多少个部分？
如图④,平面中画出 $ 1 $ 个圆时,最多可以把平面分割成 $ 2 $ 个部分；如图⑤,平面中画出第 $ 2 $ 个圆时,新增的一个圆与已知的 $ 1 $ 个圆最多有 $ 2 $ 个交点,这 $ 2 $ 个交点会把新增的这个圆分成 $ 2 $ 部分,从而多出 $ 2 $ 个部分,即总共会得到 $ 1 + 1 + 2 = 4 $(个)部分,所以 $ 2 $ 个圆最多可以把平面分割成 $ 4 $ 个部分；如图⑥,平面中画出第 $ 3 $ 个圆时,新增的一个圆与已知的 $ 2 $ 个圆最多有 $ 4 $ 个交点,这 $ 4 $ 个交点会把新增的这个圆分成 $ 4 $ 部分,从而多出 $ 4 $ 个部分,即总共会得到 $ 1 + 1 + 2 + 4 = 8 $(个)部分……
问题二：$ 5 $ 个圆最多可以把平面分割成个部分。

(3) 探究三,拓展延伸：
问题三：$ 5 $ 条直线和 $ 1 $ 个圆最多可以把平面分割成多少个部分？请结合以上探究过程说明理由。

3. 平面上有 $ 10 $ 条直线,无任何 $ 3 $ 条交于一点,要使它们出现 $ 31 $ 个交点,怎样安排才能实现？试画出图形。