2025年学霸题中题七年级数学上册苏科版第166页解析答案

8. 如图,在同一平面内,$∠AOB= 90^{\circ}$,若$∠AOC= ∠BOD= 30^{\circ}$,则$∠COD$的度数不可能为( )

A.$30^{\circ}$
B.$90^{\circ}$
C.$120^{\circ}$
D.$150^{\circ}$

答案：
C 解析:当 $OC$, $OD$ 都在 $\angle AOB$ 的内部时,如图①所示,此时 $\angle COD = \angle AOB - \angle AOC - \angle BOD = 90^{\circ} - 30^{\circ} - 30^{\circ} = 30^{\circ}$,故 A 不符合题意;当 $OC$, $OD$ 都在 $\angle AOB$ 的外部时,如图②所示,此时 $\angle COD = \angle AOB + \angle AOC + \angle BOD = 90^{\circ} + 30^{\circ} + 30^{\circ} = 150^{\circ}$,故 D 不符合题意;当 $OC$, $OD$ 任一个在 $\angle AOB$ 内部,另一个在 $\angle AOB$ 的外部时,如图③和图④所示,此时 $\angle COD = \angle AOB + \angle AOC - \angle BOD = 90^{\circ} + 30^{\circ} - 30^{\circ} = 90^{\circ}$ 或 $\angle COD = \angle AOB - \angle AOC + \angle BOD = 90^{\circ} - 30^{\circ} + 30^{\circ} = 90^{\circ}$,故 B 不符合题意,故选 C.
　　　　　　

9. 直线$AB$,$CD相交于点O$,$∠AOC= 30^{\circ}$,若$OE⊥AB$,$OF平分∠DOE$,则$∠COF$的度数为____。

答案：
$120^{\circ}$ 或 $150^{\circ}$ 解析:(1)当射线 $OE$ 在直线 $AB$ 上方时,如图①. 因为 $OE \perp AB$,所以 $\angle BOE = 90^{\circ}$. 因为 $\angle AOC = 30^{\circ}$,所以 $\angle BOD = 30^{\circ}$,所以 $\angle DOE = \angle BOD + \angle BOE = 120^{\circ}$. 因为 $OF$ 平分 $\angle DOE$,所以 $\angle DOF = \frac{1}{2}\angle DOE = \frac{1}{2} × 120^{\circ} = 60^{\circ}$,所以 $\angle COF = 180^{\circ} - \angle DOF = 120^{\circ}$.
　　　　

(2)当射线 $OE$ 在直线 $AB$ 下方时,如图②. 因为 $OE \perp AB$,所以 $\angle BOE = 90^{\circ}$. 因为 $\angle AOC = 30^{\circ}$,所以 $\angle BOD = 30^{\circ}$,所以 $\angle DOE = \angle BOE - \angle BOD = 90^{\circ} - 30^{\circ} = 60^{\circ}$. 因为 $OF$ 平分 $\angle DOE$,所以 $\angle DOF = \frac{1}{2}\angle DOE = \frac{1}{2} × 60^{\circ} = 30^{\circ}$,所以 $\angle COF = 180^{\circ} - \angle DOF = 150^{\circ}$. 综上, $\angle COF$ 的度数为 $120^{\circ}$ 或 $150^{\circ}$.

10. 若$∠AOB= 80^{\circ}$,过点$O作射线OC$(不同于$OA$,$OB$),满足$∠AOC= \frac {3}{5}∠BOC$,则$∠AOC$的大小为____。(注：题中所说的角都是小于平角的角)

答案：
$30^{\circ}$ 或 $105^{\circ}$ 解析:(1)当 $OC$ 落在 $\angle AOB$ 内部时,如图①,因为 $\angle AOC = \frac{3}{5}\angle BOC$, $\angle AOB = 80^{\circ}$,所以 $\angle AOC = 80^{\circ} × \frac{3}{8} = 30^{\circ}$.
　　　　　

(2)当 $OC$ 落在 $\angle AOB$ 外部时,如图②,反向延长 $OA$, $OB$.
①若 $OC$ 落在 $\angle BON$ 内,则 $\angle AOC \gt \angle BOC$. 因为 $\angle AOC = \frac{3}{5}\angle BOC$,所以这种情况不存在.
②若 $OC$ 落在 $\angle MOA$ 内,则 $\angle BOC - \angle AOC = 80^{\circ}$. 因为 $\angle AOC : \angle BOC = 3 : 5$,所以 $\angle BOC = 200^{\circ} \gt 180^{\circ}$,所以这种情况不存在.
③若 $OC$ 落在 $\angle MON$ 内,则 $\angle AOC + \angle BOC = 360^{\circ} - 80^{\circ} = 280^{\circ}$,所以 $\angle AOC = 280^{\circ} × \frac{3}{8} = 105^{\circ}$.
综上所述, $\angle AOC = 30^{\circ}$ 或 $105^{\circ}$.

11. (2025·阜阳期末)如图,已知$∠AOB与∠BOC$互余,且$∠AOB= 2∠BOC$。若$∠AOE= 40^{\circ}$,请补全图形,求$∠BOE$的度数。

答案：
因为 $\angle AOB$ 与 $\angle BOC$ 互余,所以 $\angle AOB + \angle BOC = 90^{\circ}$.
又 $\angle AOB = 2\angle BOC$,即 $\angle BOC = \frac{1}{2}\angle AOB$,所以 $\angle AOB + \frac{1}{2}\angle AOB = 90^{\circ}$,解得 $\angle AOB = 60^{\circ}$. 当 $OE$ 在 $\angle AOB$ 的外部时,如图①所示,因为 $\angle AOE = 40^{\circ}$,所以 $\angle BOE = \angle AOE + \angle AOB = 100^{\circ}$.
　　　　　　　

当 $OE$ 在 $\angle AOB$ 的内部时,如图②所示,因为 $\angle AOE = 40^{\circ}$,所以 $\angle BOE = \angle AOB - \angle AOE = 20^{\circ}$. 综上所述, $\angle BOE$ 的度数为 $100^{\circ}$ 或 $20^{\circ}$.

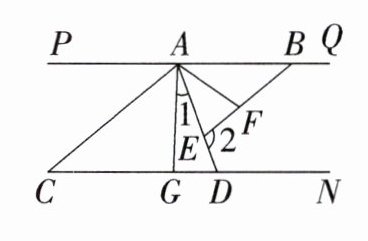
12. “中欧铁路”为了安全起见在某段铁路两旁安置了$A$,$D$两座可旋转探照灯。假定主道路是平行的,即$PQ// CN$,$A$,$B为PQ$上两点,$AD平分∠CAB交CN于点D$,$E为AD$上一点,连接$BE$,$AF平分∠BAD交BE于点F$。
(1)若$∠C= 40^{\circ}$,求$∠EAP$的大小。
(2)作$AG交CD于点G$,且满足$∠1= \frac {1}{3}∠ADC$,当$∠2+\frac {6}{5}∠GAF= 180^{\circ}$时,试说明：$AC// BE$。
(3)在(1)的条件下,探照灯$A$,$D$照出的光线在铁路所在平面旋转,探照灯$A射出的光线AC$以每秒4度的速度逆时针转动,探照灯$D射出的光线DN$以每秒12度的速度逆时针转动,光线$DN转至射线DC$后立即以相同速度顺时针回转,若它们同时开始转动,设转动时间为$t$秒,当光线$DN$回到出发时的位置时同时停止转动,则在转动过程中,$t为何值时光线AC与光线DN$互相平行或垂直？请直接写出$t$的值。

答案：
(1)因为 $PQ // CN$, $\angle C = 40^{\circ}$,所以 $\angle CAB + \angle C = 180^{\circ}$, $\angle PAC = \angle C = 40^{\circ}$,所以 $\angle CAB = 140^{\circ}$. 因为 $AD$ 平分 $\angle CAB$,所以 $\angle CAD = \frac{1}{2}\angle CAB = \frac{1}{2} × 140^{\circ} = 70^{\circ}$,所以 $\angle EAP = \angle CAD + \angle PAC = 70^{\circ} + 40^{\circ} = 110^{\circ}$.
(2)因为 $PQ // CN$,所以 $\angle ADC = \angle BAD$. 因为 $\angle 1 = \frac{1}{3}\angle ADC$,所以 $\angle 1 = \frac{1}{3}\angle BAD$. 因为 $AF$ 平分 $\angle BAD$,所以 $\angle BAD = 2\angle EAF$,所以 $\angle 1 = \frac{2}{3}\angle EAF$,所以 $\angle GAF = \angle 1 + \angle EAF = \frac{5}{3}\angle EAF$. 因为 $\angle 2 + \frac{6}{5}\angle GAF = 180^{\circ}$,所以 $\angle 2 + 2\angle EAF = 180^{\circ}$,所以 $\angle 2 + \angle BAD = 180^{\circ}$. 因为 $\angle 2 + \angle AEB = 180^{\circ}$,所以 $\angle BAD = \angle AEB$. 因为 $\angle BAD = \angle CAD$,所以 $\angle CAD = \angle AEB$,所以 $AC // BE$.
(3)$t$ 的值为 5 或 20 或 $\frac{205}{8}$. 解析:$360^{\circ} ÷ 12^{\circ} = 30$(s),当 $AC // DN$ 时,则 $\angle ACD = \angle HDN$,如图①,因为 $PQ // CH$,所以 $\angle PAC = \angle ACD$,所以 $\angle PAC = \angle HDN$. 由题意得 $\angle PAC = 40^{\circ} + 4t^{\circ}$, $\angle HDN = 12t^{\circ}$,所以 $40^{\circ} + 4t^{\circ} = 12t^{\circ}$,所以 $t = 5$.
　　　　

当 $AC \perp DN$ 时, $\angle CND = 90^{\circ}$,如图②,因为 $PA // CD$,所以 $\angle ACD = \angle PAC = 40^{\circ} + 4t^{\circ}$.
当 $t \lt 15$ 时,光线 $DN$ 未转至射线 $DC$,有 $\angle NDH = 12t^{\circ}$,所以 $\angle NDC = 180^{\circ} - 12t^{\circ}$,所以 $40^{\circ} + 4t^{\circ} + 180^{\circ} - 12t^{\circ} = 90^{\circ}$,解得 $t = \frac{65}{4}$. 因为 $\frac{65}{4} \gt 15$,故不符合题意;当 $t \geqslant 15$ 时,光线 $DN$ 顺时针回转,有 $\angle NDC = 12t^{\circ} - 180^{\circ}$,所以 $40^{\circ} + 4t^{\circ} + 12t^{\circ} - 180^{\circ} = 90^{\circ}$,解得 $t = \frac{115}{8}$. 因为 $\frac{115}{8} \lt 15$,故不符合题意.
当 $ND // AC$ 时,则 $\angle NDC = \angle ACH$,如图③,由题意, $\angle MDN = 12t^{\circ} - 180^{\circ}$, $\angle PAC = 40^{\circ} + 4t^{\circ}$,所以 $\angle NDC = 180^{\circ} - \angle MDN = 360^{\circ} - 12t^{\circ}$. 因为 $PA // CD$,所以 $\angle ACH = \angle PAC = 40^{\circ} + 4t^{\circ}$,所以 $40^{\circ} + 4t^{\circ} = 360^{\circ} - 12t^{\circ}$,所以 $t = 20$.
　　　　

当 $DN \perp AC$ 时, $\angle DNC = 90^{\circ}$,如图④,因为 $\angle NDC = 360^{\circ} - 12t^{\circ}$, $\angle NDC + \angle DCN = 90^{\circ}$, $\angle DCN = 180^{\circ} - (40^{\circ} + 4t^{\circ})$,所以 $360^{\circ} - 12t^{\circ} + 180^{\circ} - (40^{\circ} + 4t^{\circ}) = 90^{\circ}$,所以 $t = \frac{205}{8}$.
综上,$t$ 的值为 5 或 20 或 $\frac{205}{8}$.