1. 如图,若$∠AOM= α$,$∠BOC= 4∠BON$,$OM平分∠CON$,则$∠MON$的度数为
$\frac{540^{\circ}-3\alpha}{5}$
。
答案:$\frac{540^{\circ}-3\alpha}{5}$ 解析:设 $\angle BON = x$,则 $\angle BOC = 4x$,所以 $\angle CON = \angle COB - \angle BON = 4x - x = 3x$. 因为 $OM$ 平分 $\angle CON$,所以 $\angle MON = \frac{1}{2}\angle CON = \frac{3}{2}x$. 因为 $\angle AOM = \alpha$,所以 $\angle BOM = \angle MON + \angle BON = \frac{3}{2}x + x = 180^{\circ} - \alpha$,所以 $x = \frac{360^{\circ}-2\alpha}{5}$. 所以 $\angle MON = \frac{3}{2}x = \frac{3}{2} × \frac{360^{\circ}-2\alpha}{5} = \frac{540^{\circ}-3\alpha}{5}$,即 $\angle MON$ 的度数为 $\frac{540^{\circ}-3\alpha}{5}$.
解析:
解:设$\angle BON = x$,则$\angle BOC = 4x$,$\angle CON=\angle BOC - \angle BON=4x - x = 3x$。
因为$OM$平分$\angle CON$,所以$\angle MON=\frac{1}{2}\angle CON=\frac{3}{2}x$。
因为$\angle AOM = \alpha$,$\angle AOB = 180^{\circ}$,所以$\angle BOM=180^{\circ}-\alpha$。
又因为$\angle BOM=\angle MON+\angle BON=\frac{3}{2}x + x=\frac{5}{2}x$,所以$\frac{5}{2}x=180^{\circ}-\alpha$,解得$x=\frac{2(180^{\circ}-\alpha)}{5}=\frac{360^{\circ}-2\alpha}{5}$。
因此$\angle MON=\frac{3}{2}x=\frac{3}{2}×\frac{360^{\circ}-2\alpha}{5}=\frac{540^{\circ}-3\alpha}{5}$。
故$\angle MON$的度数为$\frac{540^{\circ}-3\alpha}{5}$。
2. 某人傍晚6点多外出购物,当时表上的时针与分针的较小夹角恰好为$110^{\circ}$,傍晚不到7点回家时,发现表上的时针与分针的较小夹角又是$110^{\circ}$,试算出此人外出用了多长时间。
答案:解法一:设此人外出用了 $x$ 分钟,则分针走了 $6x^{\circ}$,时针走了 $0.5x^{\circ}$,由题意,得 $6x - 0.5x = 110 × 2$,解得 $x = 40$. 故此人外出用了 40 分钟.
解法二:设此人是 6 时 $x$ 分外出的,则有 $180 + 0.5x - 6x = 110$,解得 $x = 12\frac{8}{11}$,即此人是 6 时 $12\frac{8}{11}$ 分外出的.
设此人是 6 时 $y$ 分回家的,则有 $6y - 180 - 0.5y = 110$,解得 $y = 52\frac{8}{11}$,即此人是 6 时 $52\frac{8}{11}$ 分回家的. 所以 $52\frac{8}{11} - 12\frac{8}{11} = 40$(分钟),即此人外出用了 40 分钟.
3. 已知$∠AOB= 150^{\circ}$,$OC是∠AOB$内的一条射线,射线$OD平分∠AOC$,射线$OE平分∠BOD$。
(1)如图①,若$∠AOD= ∠EOC$,求$∠AOD$的度数;
(2)若$∠AOD= α(α≠50^{\circ})$,求$\frac {|∠AOD-∠BOE|}{∠COE}$的值。
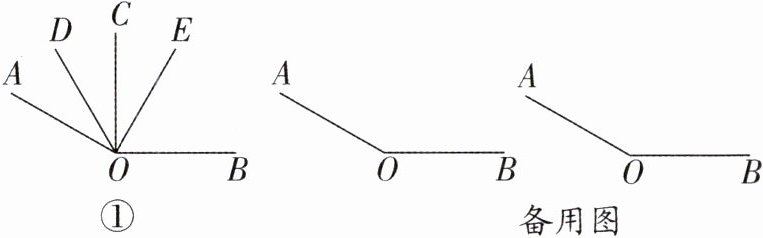
答案:(1)设 $\angle AOD = \alpha$. 因为 $\angle AOD = \angle EOC$,所以 $\angle EOC = \alpha$. 因为 $\angle AOB = 150^{\circ}$,所以 $\angle BOD = \angle AOB - \angle AOD = 150^{\circ} - \alpha$. 因为射线 $OD$ 平分 $\angle AOC$,所以 $\angle DOC = \angle AOD = \alpha$. 所以 $\angle BOE = \angle AOB - \angle AOD - \angle DOC - \angle EOC = 150^{\circ} - 3\alpha$. 因为射线 $OE$ 平分 $\angle BOD$,所以 $\angle BOE = \frac{1}{2}\angle BOD = \frac{150^{\circ}-\alpha}{2}$,所以 $\frac{150^{\circ}-\alpha}{2} = 150^{\circ} - 3\alpha$,解得 $\alpha = 30^{\circ}$,即 $\angle AOD = 30^{\circ}$.
(2)当 $\alpha \lt 50^{\circ}$ 时,如图①,因为 $\angle AOD = \alpha$, $\angle BOE = \frac{1}{2}\angle BOD = \frac{150^{\circ}-\alpha}{2}$,所以 $\angle COE = \angle BOC - \angle BOE = 150^{\circ} - 2\alpha - \frac{150^{\circ}-\alpha}{2} = \frac{150^{\circ}-3\alpha}{2}$,所以 $\frac{|\angle AOD - \angle BOE|}{\angle COE} = \frac{\left|\alpha - \frac{150^{\circ}-\alpha}{2}\right|}{\frac{150^{\circ}-3\alpha}{2}} = \frac{|3\alpha - 150^{\circ}|}{150^{\circ}-3\alpha} = \frac{150^{\circ}-3\alpha}{150^{\circ}-3\alpha} = 1$.


当 $\alpha \gt 50^{\circ}$ 时,如图②,因为 $\angle AOD = \alpha$, $\angle BOE = \frac{1}{2}\angle BOD = \frac{150^{\circ}-\alpha}{2}$,所以 $\angle COE = \angle BOE - \angle BOC = \frac{150^{\circ}-\alpha}{2} - (150^{\circ} - 2\alpha) = \frac{3\alpha - 150^{\circ}}{2}$,所以 $\frac{|\angle AOD - \angle BOE|}{\angle COE} = \frac{\left|\alpha - \frac{150^{\circ}-\alpha}{2}\right|}{\frac{3\alpha - 150^{\circ}}{2}} = \frac{|3\alpha - 150^{\circ}|}{3\alpha - 150^{\circ}} = \frac{3\alpha - 150^{\circ}}{3\alpha - 150^{\circ}} = 1$. 综上,若 $\angle AOD = \alpha(\alpha \neq 50^{\circ})$,则 $\frac{|\angle AOD - \angle BOE|}{\angle COE} = 1$.
4. (2025·南阳校级月考)将一张正方形纸片$ABCD$按如图所示的方式折叠,$AE$,$AF$为折痕,点$B$,$D折叠后的对应点分别为B'$,$D'$,若$∠B'AD'= 16^{\circ}$,则$∠EAF$的度数为(
D
)
A.$40^{\circ}$
B.$45^{\circ}$
C.$56^{\circ}$
D.$37^{\circ}$
答案:D 解析:因为四边形 $ABCD$ 为正方形,所以 $\angle DAB = 90^{\circ}$,由翻折的性质可知, $\angle BAE = \angle B'AE$, $\angle DAF = \angle D'AF$,所以 $2\angle DAF + 2\angle BAE = \angle DAB + \angle B'AD'$,即 $2(\angle DAF + \angle BAE) = 90^{\circ} + 16^{\circ}$,解得 $\angle DAF + \angle BAE = 53^{\circ}$,所以 $\angle EAF = 90^{\circ} - (\angle DAF + \angle BAE) = 37^{\circ}$,故选 D.
5. 如图,在平面内,$∠AOB= 90^{\circ}$,$OC在∠AOB$的外部,$∠COB$是锐角,$OP平分∠AOC$,$OQ平分∠COB$,若$∠COB$的度数逐渐变大,则$∠POQ$的变化情况是(
C
)
A.变大
B.变小
C.保持不变
D.无法确定
答案:C 解析:因为 $OP$ 平分 $\angle AOC$, $OQ$ 平分 $\angle COB$,所以 $\angle COP = \frac{1}{2}\angle AOC$, $\angle COQ = \frac{1}{2}\angle BOC$,所以 $\angle POQ = \angle COP - \angle COQ = \frac{1}{2}\angle AOC - \frac{1}{2}\angle BOC = \frac{1}{2}(\angle AOC - \angle BOC) = \frac{1}{2}\angle AOB = \frac{1}{2} × 90^{\circ} = 45^{\circ}$,所以 $\angle POQ$ 的度数不变. 故选 C.
6. 如图,将三个相同的三角尺$60^{\circ}$角的顶点重合放置,如果$∠1= 22^{\circ}$,$∠2= 26^{\circ}$,那么$∠3$的度数是____。

答案:$12^{\circ}$ 解析:如图,因为 $\angle 1 + \angle 4 + \angle 2 = \angle 4 + \angle 2 + \angle 5 = 60^{\circ}$,所以 $\angle 5 = \angle 1 = 22^{\circ}$. 因为 $\angle 2 + \angle 5 + \angle 3 = 60^{\circ}$,所以 $\angle 3 = 60^{\circ} - \angle 5 - \angle 2 = 12^{\circ}$.

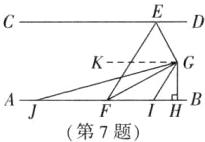
7. 如图,$AB// CD$,$EG平分∠DEF$,$FG平分∠BFE$。
(1)试说明:$∠EFG+∠GEF= 90^{\circ}$;
(2)在(1)的条件下,过点$G作GH⊥AB$,垂足为$H$,$∠FGH的平分线GI交AB于点I$,$∠EGH的平分线GJ交AB于点J$,求$∠IGJ$的度数。

答案:(1)因为 $AB // CD$,所以 $\angle DEF + \angle BFE = 180^{\circ}$. 因为 $EG$ 平分 $\angle DEF$, $FG$ 平分 $\angle BFE$,所以 $\angle DEF = 2\angle GEF = 2\angle DEG$, $\angle BFE = 2\angle EFG = 2\angle GFB$,所以 $2\angle GEF + 2\angle EFG = 180^{\circ}$,所以 $\angle EFG + \angle GEF = 90^{\circ}$.
(2)如图,过点 $G$ 作 $GK // AB$. 因为 $AB // CD$,所以 $AB // GK // CD$,所以 $\angle DEG = \angle EGK$, $\angle KGF = \angle GFB$. 由(1)得 $\angle EFG + \angle GEF = 90^{\circ}$,所以 $\angle EGK + \angle KGF = 90^{\circ}$. 因为 $GH \perp AB$,所以 $GH \perp KG$,即 $\angle KGH = \angle KGF + \angle HGF = 90^{\circ}$,所以 $\angle EGK = \angle HGF$. 因为 $GJ$ 平分 $\angle EGH$,所以 $\angle EGJ = \angle HGJ$. 又 $\angle KGJ = \angle EGJ - \angle EGK$, $\angle FGJ = \angle HGJ - \angle HGF$,所以 $\angle KGJ = \angle FGJ$,所以 $\angle KGF = 2\angle FGJ$. 因为 $GI$ 平分 $\angle HGF$,所以 $\angle HGF = 2\angle FGI$,所以 $2\angle FGJ + 2\angle FGI = 90^{\circ}$,即 $\angle FGJ + \angle FGI = 45^{\circ}$,所以 $\angle IGJ = \angle FGJ + \angle FGI = 45^{\circ}$.