2025年学霸题中题七年级数学上册苏科版第164页解析答案

3. (2025·上海期中) 如图,$CD // AB$,现将一块含$30^{\circ}的三角板EFG$按如图①放置,$\angle G = 90^{\circ}$,$\angle EFG = 30^{\circ}$,使点$E$,$F分别在直线CD$,$AB$上,设$\angle GFB = \alpha(0^{\circ} ＜ \alpha ＜ 90^{\circ})$。
(1) 求$\angle DEG + \angle GFB$的度数。
(2) 如果$\angle CEF的平分线EH交直线AB于点H$,如图②。
①当$EH // FG$时,求$\alpha$的度数；
②在①的条件下,如果点$P是射线EC$上的一点,将三角板$EFG绕点E以每秒1^{\circ}$的速度进行顺时针旋转,同时射线$PC绕点P以每秒4^{\circ}$的速度进行顺时针旋转,射线$PC$旋转一周后停止转动,同时三角板$EFG$也停止转动。当旋转多少时间时,$CP与\triangle EFG$的一边平行？

答案：
3.(1)如图①,过点G作GM//AB,因为CD//AB,MG//AB,所以CD//MG,所以∠MGF = ∠BFG,∠DEG = ∠EGM,所以∠DEG + ∠BFG = ∠EGM + ∠MGF = ∠EGF = 90°,所以∠DEG + ∠BFG = 90°.
　　　　　　　　　

(2)①因为EH//FG,所以∠GFB = ∠EHF = α.因为EH平分∠CEF,所以∠CEH = ∠FEH.又因为CD//AB,所以∠CEH = ∠EHF = α,∠CEF = ∠EFB = 2α,所以2α = 30° + α,解得α = 30°.
②如图②,当PC'//EG时,延长GE至点Q,因为PC'//GQ,所以∠CPC' = ∠CEQ.因为∠CEQ = ∠DEG,所以∠CPC' = ∠DEG,由题意知∠CPC' = (4t)°,由①得∠DEG = 60° + t°,所以(4t)° = 60° + t°,解得t = 20.
　　　　

如图③,当PC'//EF时,所以∠CPC' = ∠DEF,由题意得∠DEF = ∠DEG + ∠FEG = 120° + t°,所以(4t)° = 120° + t°,解得t = 40;
如图④,当PC'//FG时,延长GF交CE于点T,过点G作GV//CD,所以∠VGE = ∠DEG = 60° + t°.因为∠FGE = 90°,所以∠VGT = t° - 30°,所以∠ETG = ∠VGT = t° - 30°.因为PC'//FG,所以∠DPC' = ∠ETG = t° - 30°.因为∠DPC' = (4t)° - 180°,所以(4t)° - 180° = t° - 30°,解得t = 50.
　　　　

如图⑤,当PC'//EG(第二次)时,则∠CPC' = ∠CEG,所以360° - (4t)° = 180° - (60° + t°),解得t = 80.
综上,当旋转20秒或40秒或50秒或80秒时,CP与△EFG的一边平行

4. (2025·成都期末) 已知$\angle AOB = 90^{\circ}$。
(1) 如图①,若射线$ON$,$OM分别为\angle AOC$,$\angle BOC$的平分线,则$\angle MON = $______。
(2) 如图②,射线$OC从OA出发绕点O以每秒20^{\circ}$的速度沿逆时针方向旋转,射线$OD从OA出发绕点O以每秒10^{\circ}$的速度沿顺时针方向旋转,设运动时间为$t$秒,且$OM平分\angle BOC$。
①当$0 ＜ t ＜ 4.5$时,若$ON分\angle AOC为1:3$两个部分,求满足$\angle DON = \frac{1}{2}\angle MON$时,$t$的值。
②如图③,若$OP平分\angle AOD$,当$0 ＜ t ＜ 6且t \neq 4.5$时,试判断$2\angle MOP - \angle COD$是否为定值。若是,请求出该定值；若不是,请说明理由。

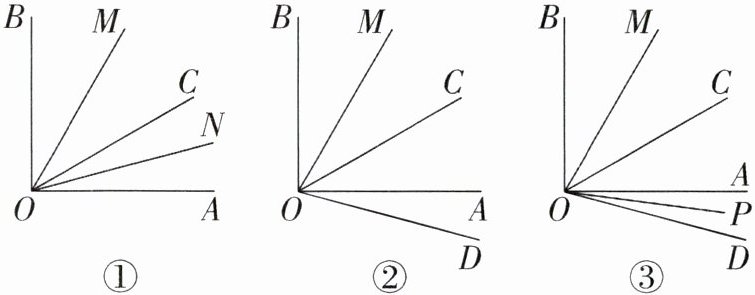
答案：
4.(1)45°　解析:如图①,∠AOB = 90°,则∠AOC + ∠BOC = 90°.因为射线ON,OM分别为∠AOC,∠BOC的平分线,所以∠CON = $\frac{1}{2}$∠AOC,∠MOC = $\frac{1}{2}$∠BOC,所以∠MON = ∠CON + ∠MOC = $\frac{1}{2}$(∠AOC + ∠BOC) = $\frac{1}{2}$×90° = 45°.
　　　　　　　　　　

(2)①如图②,因为射线OC从OA出发绕点O以每秒20°的速度沿逆时针方向旋转，射线OD从OA出发绕点O以每秒10°的速度沿顺时针方向旋转，运动时间为t秒,所以∠AOC = (20t)°,∠AOD = (10t)°,所以∠BOC = 90° - (20t)°.因为OM平分∠BOC,ON分∠AOC为1:3两个部分,所以∠COM = $\frac{1}{2}$∠BOC = 45° - (10t)°,∠AON = $\frac{1}{4}$∠AOC = (5t)°,∠CON = $\frac{3}{4}$∠AOC = (15t)°或∠AON = $\frac{3}{4}$∠AOC = (15t)°,∠CON = $\frac{1}{4}$∠AOC = (5t)°.当∠AON = $\frac{1}{4}$∠AOC = (5t)°,∠CON = $\frac{3}{4}$∠AOC = (15t)°时,所以∠DON = ∠AON + ∠AOD = (5t)° + (10t)° = (15t)°,∠MON = ∠COM + ∠CON = 45° - (10t)° + (15t)° = 45° + (5t)°.因为∠DON = $\frac{1}{2}$∠MON,所以(15t)° = $\frac{1}{2}$[45° + (5t)°],解得t = $\frac{9}{5}$;
当∠AON = $\frac{3}{4}$∠AOC = (15t)°,∠CON = $\frac{1}{4}$∠AOC = (5t)°时,所以∠DON = ∠AON + ∠AOD = (15t)° + (10t)° = (25t)°,∠MON = ∠COM + ∠CON = 45° - (10t)° + (5t)° = 45° - (5t)°.因为∠DON = $\frac{1}{2}$∠MON,所以(25t)° = $\frac{1}{2}$[45° - (5t)°],解得t = $\frac{9}{11}$
综上所述，t的值为$\frac{9}{5}$或$\frac{9}{11}$
　　　　

②当0 ＜ t ＜ 4.5时,如图③,∠AOC = (20t)°,∠AOD = (10t)°,∠BOC = 90° - (20t)°,因为OM平分∠BOC,OP平分∠AOD,所以∠MOC = $\frac{1}{2}$∠BOC = 45° - (10t)°,∠AOP = $\frac{1}{2}$∠AOD = (5t)°,所以∠MOP = ∠MOC + ∠AOC + ∠AOP = 45° - (10t)° + (20t)° + (5t)° = 45° + (15t)°,∠COD = ∠AOC + ∠AOD = (20t)° + (10t)° = (30t)°,所以2∠MOP - ∠COD = 2[45° + (15t)°] - (30t)° = 90°,为定值;
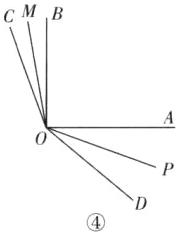
当4.5 ＜ t ＜ 6时,如图④,∠AOC = (20t)°,∠AOD = (10t)°,∠BOC = (20t)° - 90°,因为OM平分∠BOC,OP平分∠AOD,所以∠MOB = $\frac{1}{2}$∠BOC = (10t)° - 45°,∠AOP = $\frac{1}{2}$∠AOD = (5t)°,所以∠MOP = ∠MOB + ∠AOB + ∠AOP = (10t)° - 45° + 90° + (5t)° = 45° + (15t)°,∠COD = ∠AOC + ∠AOD = (20t)° + (10t)° = (30t)°,所以2∠MOP - ∠COD = 2[45° + (15t)°] - (30t)° = 90°,为定值.
综上所述,2∠MOP - ∠COD = 90°,为定值
　　　　　　　　