2025年学霸题中题七年级数学上册苏科版第162页解析答案

1. 已知 O 为直线 AB 上一点,过点 O 向直线 AB 上方引两条射线 OC,OD,且 OC 平分∠AOD.
(1) 若∠BOD:∠AOD = 4:6,求∠AOC 的度数.
(2) 请在图①中画一条射线 OE,使得 OE 平分∠BOD,并求此时∠COE 的度数.
(3) 将(2)中的射线 OE 绕点 O 旋转一定的角度,使得∠BOE = 4∠DOE,且∠COE = 75°,求此时∠BOE 的度数.

答案：
1. (1) 因为∠BOD:∠AOD = 4:6，且∠AOD + ∠BOD = 180°，所以∠AOD = $\frac{3}{5}$×180° = 108°。因为OC平分∠AOD，所以∠AOC = $\frac{1}{2}$∠AOD = $\frac{1}{2}$×108° = 54°。
(2) 如图①所示，OE即为所求。

因为OC平分∠AOD，OE平分∠BOD，所以∠COD = $\frac{1}{2}$∠AOD，∠EOD = $\frac{1}{2}$∠BOD，所以∠COE = ∠COD + ∠EOD = $\frac{1}{2}$(∠AOD + ∠BOD) = $\frac{1}{2}$×180° = 90°。
(3) 当射线OE在∠BOD内部时，如图②，设∠1 = α，根据题意得∠2 = 4∠1 = 4α。因为∠COE = ∠1 + ∠3 = 75°，所以∠3 = 75° - α。因为OC平分∠AOD，所以∠4 = ∠3 = 75° - α。因为∠1 + ∠2 + ∠3 + ∠4 = 180°，所以α + 4α + 75° - α + 75° - α = 180°，解得α = 10°，所以∠2 = 4α = 40°，所以∠BOE = 40°。

当射线OE在∠BOD外部时，如图③，因为∠BOE = 4∠DOE，设∠DOE = α，则∠DOB = 3α。所以∠AOD = 180° - ∠DOB = 180° - 3α。因为OC平分∠AOD，所以∠COD = $\frac{1}{2}$∠AOD = 90° - $\frac{3}{2}$α，所以∠COE = ∠COD - ∠EOD = 90° - $\frac{3}{2}$α - α = 90° - $\frac{5}{2}$α。因为∠COE = 75°，所以90° - $\frac{5}{2}$α = 75°，所以α = 6°，所以∠BOE = 4α = 24°。综上所述，∠BOE = 40°或24°。

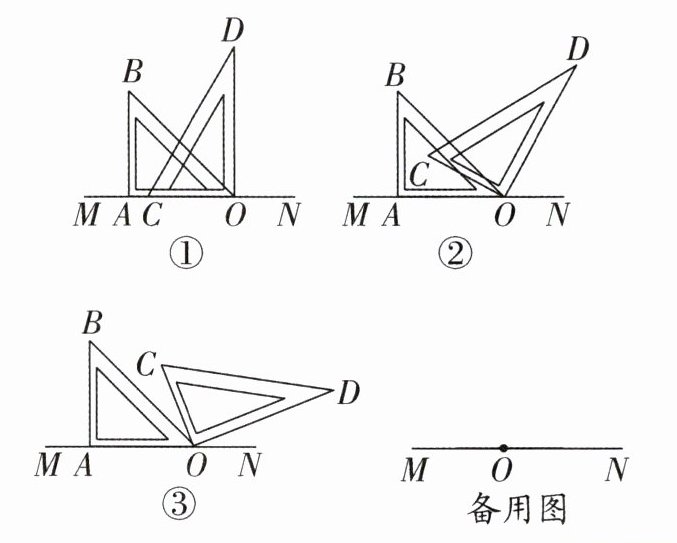
2. (2025·潍坊期末)将一副三角板按如图①所示摆放,点 A,C,O 在直线 MN 上,现将三角板进行下面的操作.
操作一:保持三角板 AOB 位置不动,将三角板 COD 绕点 O 顺时针旋转(如图②,图③),当三角板 COD 的边 OD 第一次与直线 MN 重合时旋转停止.
思考并回答下列问题:
(1) 当∠MOC = ______°时,OC 是∠MOB 的一条三等分线.
(2) 如图②,当 OC,OD 位于直线 OB 的两侧时,∠DOB 与∠MOC 的数量关系是______.
(3) 如图③,当 OC,OD 位于直线 OB 的同侧时,(2)中结论是否仍然成立? 若成立,请说明理由;若不成立,请写出正确的结论,并说明理由.
操作二:在三角板 COD 绕点 O 开始顺时针旋转的同时,另一个三角板 AOB 也绕点 O 顺时针旋转,当三角板 COD 的边 OC 第一次与直线 MN 重合时,两三角板同时停止旋转.
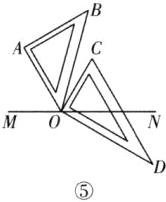
(4) 若在旋转过程中,∠MOC 始终是∠MOA 的 2 倍,请直接写出∠DOB 与∠MOC 的数量关系.

答案：
2. (1) 15或30 解析：如图①，当∠MOC = $\frac{1}{3}$∠MOB时，则∠MOC = $\frac{1}{3}$×45° = 15°；

如图②，当∠BOC = $\frac{1}{3}$∠MOB时，则∠BOC = $\frac{1}{3}$×45° = 15°，此时∠MOC = ∠MOB - ∠BOC = 45° - 15° = 30°。故答案为15或30。
(2) ∠DOB - ∠MOC = 45°
(3) 成立，理由如下：如图③，因为∠MOB = 45°，所以∠MOC = ∠MOB + ∠BOC = 45° + ∠BOC，所以∠BOC = ∠MOC - 45°。因为∠DOC = 90°，所以∠DOB = ∠DOC + ∠BOC = 90° + ∠BOC，所以∠DOB = 90° + ∠MOC - 45°，所以∠DOB - ∠MOC = 45°。

(4) 2∠DOB - ∠MOC = 90°。解析：①如图④，当OC，OD位于直线OB的两侧时，因为∠MOC = 2∠MOA，所以∠MOA = ∠AOC = $\frac{1}{2}$∠MOC。因为∠AOB = 45°，所以∠BOC = ∠AOB - ∠AOC = 45° - ∠AOC。因为∠DOC = 90°，所以∠DOB = ∠DOC - ∠BOC = 90° - (45° - ∠AOC) = 45° + ∠AOC = 45° + $\frac{1}{2}$∠MOC，所以2∠DOB - ∠MOC = 90°。②如图⑤，当OC，OD位于直线OB的同侧时，因为∠MOC = 2∠MOA，所以∠MOA = ∠AOC = $\frac{1}{2}$∠MOC。因为∠AOB = 45°，所以∠BOC = ∠AOC - ∠AOB = ∠AOC - 45°。因为∠DOC = 90°，所以∠DOB = ∠DOC + ∠BOC = 90° + (∠AOC - 45°) = 45° + ∠AOC = 45° + $\frac{1}{2}$∠MOC，所以2∠DOB - ∠MOC = 90°。综上，2∠DOB - ∠MOC = 90°。