8. 某中学七年级数学课外兴趣小组在探究“n边形(n>3)共有多少条对角线”这一问题时,设计了如下表格:
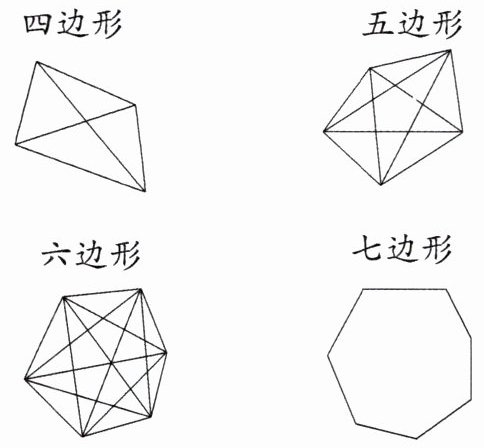
(1)请在表格中的横线上填上相应的结果.
n - 3
$\frac{n(n - 3)}{2}$
(2)求一个十二边形总共有多少条对角线.
把$n = 12$代入$\frac{n(n - 3)}{2}$计算得$\frac{12×9}{2} = 54$(条).故一个十二边形总共有54条对角线.
(3)过多边形的一个顶点的所有对角线条数与这些对角线分多边形所得的三角形个数的和可能为2024吗? 若能,请求出这个多边形的边数;若不能,请说明理由.
不可能.理由:设这个多边形的边数为n,由题意得$n - 3 + n - 2 = 2024$,解得$n = \frac{2029}{2}$,因为多边形的边数必须是整数,所以过多边形的一个顶点的所有对角线条数与这些对角线分多边形所得的三角形个数的和不可能为2024.
答案:(1)$n - 3$ $\frac{n(n - 3)}{2}$(2)把$n = 12$代入$\frac{n(n - 3)}{2}$计算得$\frac{12×9}{2} = 54$(条).故一个十二边形总共有54条对角线.(3)不可能.理由:设这个多边形的边数为n,由题意得$n - 3 + n - 2 = 2024$,解得$n = \frac{2029}{2}$,因为多边形的边数必须是整数,所以过多边形的一个顶点的所有对角线条数与这些对角线分多边形所得的三角形个数的和不可能为2024.
解析:
(1)$n - 3$;$\frac{n(n - 3)}{2}$
(2)解:当$n=12$时,$\frac{n(n - 3)}{2}=\frac{12×(12 - 3)}{2}=\frac{12×9}{2}=54$
答:一个十二边形总共有54条对角线。
(3)解:设这个多边形的边数为$n$。
由题意得:$(n - 3)+(n - 2)=2024$
$2n - 5=2024$
$2n=2029$
$n=\frac{2029}{2}=1014.5$
因为多边形的边数必须是整数,所以不能。
答:不能,因为解得的边数不是整数。
9. 若一个多边形截去一个角后,变成十四边形,则原来的多边形的边数可能为
13或14或15
.
答案:13或14或15 解析:当多边形是十五边形时,截去一个角,可能变成十四边形;当多边形是十四边形时,截去一个角,可能变成十四边形;当多边形是十三边形时,截去一个角,可能变成十四边形.所以原来的多边形的边数可能为13或14或15.
解析:
解:一个多边形截去一个角后,边数可能增加1、不变或减少1。
若边数增加1后为14,则原多边形边数为14 - 1 = 13;
若边数不变仍为14,则原多边形边数为14;
若边数减少1后为14,则原多边形边数为14 + 1 = 15。
故原来的多边形的边数可能为13或14或15。
10. 探索题:(相邻两格点的距离为1)
(1)在如图①的格点图中,各个多边形的内部都有而且只有1个格点.

将各个多边形的面积与它四周各边上格点的个数和填入下表,你能发现什么规律?
请写出S与x之间的数量关系.
(2)在如图②的格点图中,画出几个多边形,使其内部都有而且只有2个格点,再按第(1)题的做法,你发现此时各个多边形的面积S与四周各边上格点的个数和x之间又有什么样的关系呢? 请写出S与x之间的数量关系.

(3)请你继续探索,当格点多边形内部有而且只有n个格点时,猜想S与x有怎么样的关系.
答案:(1)多边形序号 1 2 3 ...多边形面积S 2 3 2 ...多边形各边上格点的个数和x 4 6 4 ...S与x之间的数量关系:$S = \frac{1}{2}x$(2)画图合理即可,如:
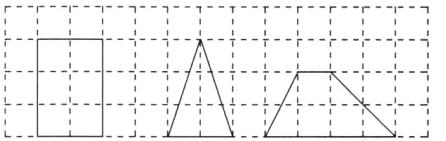
根据图可知:长方形的面积是6,它的各边上格点的个数和x是10,内部格点数是2,$6 = 10÷2 + 1$;三角形的面积是3,它的各边上格点的个数和x是4,内部格点数是2,$3 = 4÷2 + 1$;梯形的面积是5,它的各边上格点的个数和x是8,内部格点数是2,$5 = 8÷2 + 1$;那么$S = \frac{1}{2}x + 1$.(3)由图可知格点多边形内部有而且只有n个格点时,格点多边形面积=各边上格点的个数和$×\frac{1}{2} +$(多边形内部格点数 - 1),即$S = \frac{1}{2}x + (n - 1)$.