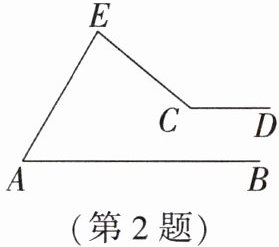
2. 如图,$∠AEC = 80^{\circ}$,在$∠AEC的两边上分别过点A和点C向同方向作射线AB和CD$,且$AB// CD$,若$∠EAB和∠ECD的平分线所在的直线交于点P$($P与C$不重合),则$∠APC$的大小为______。
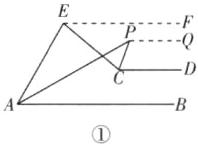
答案:$ 40^\circ $或 $ 140^\circ $ 解析:①当 $ \angle EAB $ 为锐角时,如图①所示,过点 E 作 $ EF // AB $,过点 P 作 $ PQ // AB $,因为 $ AB // CD $,所以 $ AB // CD // EF // PQ $.因为 $ EF // AB $, $ EF // CD $,所以 $ \angle EAB + \angle AEC + \angle CEF = 180^\circ $, $ \angle CEF + \angle ECD = 180^\circ $,所以 $ \angle EAB + \angle AEC = \angle ECD $,即 $ \angle ECD - \angle EAB = \angle AEC = 80^\circ $.因为 $ PQ // AB $, $ PQ // CD $,所以 $ \angle PAB + \angle APC + \angle CPQ = 180^\circ $, $ \angle CPQ + \angle PCD = 180^\circ $,所以 $ \angle PAB + \angle APC = \angle PCD $,即 $ \angle PCD - \angle PAB = \angle APC $.又因为点 P 为 $ \angle EAB $ 和 $ \angle ECD $ 的平分线所在的直线的交点,所以 $ \angle PAB = \frac{1}{2} \angle EAB $, $ \angle PCD = \frac{1}{2} \angle ECD $,所以 $ \angle APC = \angle PCD - \angle PAB = \frac{1}{2} \angle ECD - \frac{1}{2} \angle EAB = \frac{1}{2} \angle AEC = 40^\circ $.

②当 $ \angle EAB $ 为钝角时,如图②所示,过点 E 作 $ EF // AB $,过点 P 作 $ HQ // AB $,因为 $ AB // CD $,所以 $ AB // CD // EF // PQ $.因为 $ EF // AB $, $ EF // CD $,所以 $ \angle BAE + \angle AEF = 180^\circ $, $ \angle DCE + \angle CEF = 180^\circ $,所以 $ \angle BAE + \angle AEF + \angle DCE + \angle CEF = 360^\circ $.因为 $ \angle AEC = \angle AEF + \angle CEF = 80^\circ $,所以 $ \angle BAE + \angle DCE = 280^\circ $.因为 $ PQ // AB $, $ PQ // CD $,所以 $ \angle DCP = \angle HPC $, $ \angle BAP = \angle HPA $.又因为点 P 为 $ \angle EAB $ 和 $ \angle ECD $ 的平分线所在的直线的交点,所以 $ \angle BAP = \frac{1}{2} \angle BAE $, $ \angle DCP = \frac{1}{2} \angle DCE $,所以 $ \angle BAP + \angle DCP = \frac{1}{2} ( \angle BAE + \angle DCE ) = 140^\circ $,所以 $ \angle APC = \angle HPC + \angle HPA = 140^\circ $.综上所述, $ \angle APC = 40^\circ $ 或 $ 140^\circ $.