2025年学霸题中题七年级数学上册苏科版第158页解析答案

6. 如图,直线$AB// CD$,$AE\perp CE于点E$,若$∠EAB = 120^{\circ}$,则$∠ECD = $______$^{\circ}$。

答案：
6.150　解析:过点E作EF//AB,因为直线AB//CD,EF//AB,所以EF//CD,所以∠BAE + ∠FEA = 180°,∠FEC + ∠ECD = 180°,所以∠BAE + ∠FEA + ∠FEC + ∠ECD = 360°.因为∠EAB = 120°,∠AEC = 90°,所以∠ECD = 360° - (∠BAE + ∠FEA + ∠FEC) = 360° - (120° + 90°) = 150°.
一题多解
　　　如图,延长AE,与DC的延长线交于点G.因为AB//CD,所以∠A + ∠AGC = 180°.因为∠EAB = 120°,所以∠AGC = 180° - 120° = 60°.因为AE⊥CE,所以∠AEC = 90°,所以∠CEG = 180° - 90° = 90°,所以∠ECG = 180° - (∠CEG + ∠AGC) = 30°,所以∠ECD = 180° - 30° = 150°.
　　　　　　　

7. 如图是一款长臂折叠$LED$护眼灯示意图,$EF与桌面MN$垂直,当发光的灯管$AB恰好与桌面MN$平行时,$∠DEF = 120^{\circ}$,$∠BCD = 110^{\circ}$,则$∠CDE$的度数为______$^{\circ}$。

答案：
7.100　解析:因为EF⊥MN,所以∠MFE = 90°.如图,过点D作DG//AB,过点E作EH//AB.因为AB//MN,所以AB//DG//EH//MN,所以∠ACD + ∠CDG = 180°,∠HEF = ∠MFE = 90°,∠DEH = ∠GDE.因为∠DEF = 120°,∠BCD = 110°,所以∠GDE = ∠DEH = 30°,∠CDG = 180° - 110° = 70°,所以∠CDE = ∠CDG + ∠GDE = 100°.
　　　　　　　　

8. (1)如图①,$MA_{1}// NA_{2}$,则$∠A_{1} + ∠A_{2} = $______；如图②,$MA_{1}// NA_{3}$,则$∠A_{1} + ∠A_{2} + ∠A_{3} = $______,请你说明理由。
(2)如图③,$MA_{1}// NA_{4}$,则$∠A_{1} + ∠A_{2} + ∠A_{3} + ∠A_{4} = $______。
(3)利用上述结论解决问题：如图④,$AB// CD$,$∠ABE和∠CDE的平分线相交于点F$,$∠E = 140^{\circ}$,求$∠BFD$的度数。

答案：
8.(1)180° 360° 理由:如图①,过点A₂作PA₂//MA₁.因为MA₁//NA₃,所以PA₂//MA₁//NA₃,所以∠A₁ + ∠A₁A₂P = 180°,∠A₃ + ∠A₃A₂P = 180°,所以∠A₁ + ∠A₂ + ∠A₃ = 360°.
(2)540°　解析:如图②,过点A₂作PA₂//MA₁,过点A₃作QA₃//MA₁.因为MA₁//NA₄,所以QA₃//PA₂//MA₁//NA₄,所以∠A₁ + ∠A₁A₂P = 180°,∠QA₃A₂ + ∠A₃A₂P = 180°,∠A₄ + ∠A₄A₃Q = 180°,所以∠A₁ + ∠A₁A₂A₃ + ∠A₂A₃A₄ + ∠A₄ = 540°.
　

(3)如图③,过点F作FG//AB,因为AB//CD,所以AB//CD//FG,所以∠BFG = ∠ABF,∠GFD = ∠CDF.因为∠ABE和∠CDE的平分线相交于点F,所以∠BFD = $\frac{1}{2}$(∠ABE + ∠CDE).又因为∠ABE + ∠E + ∠CDE = 360°,∠E = 140°,所以∠ABE + ∠CDE = 360° - 140° = 220°,所以∠BFD = $\frac{1}{2}$×220° = 110°.

9. 如图,$B$,$C$,$D$是不在同一直线上的三点,且$∠CDE + ∠BCD - ∠ABC = 180^{\circ}$。
(1)如图①,试说明：$AB// DE$。
(2)$DG平分∠EDC$,点$P是DG$上一点,过点$P作射线PB$,设$∠1 = \alpha$。
①如图②,若$PD// BC$,$∠ABC = 2∠3$,求$∠C$的度数；(用含$\alpha$的式子表示)
②如图③,若$∠3 + \frac{1}{2}∠C = 90^{\circ}$,判断$∠1与∠2$的数量关系,并说明理由。

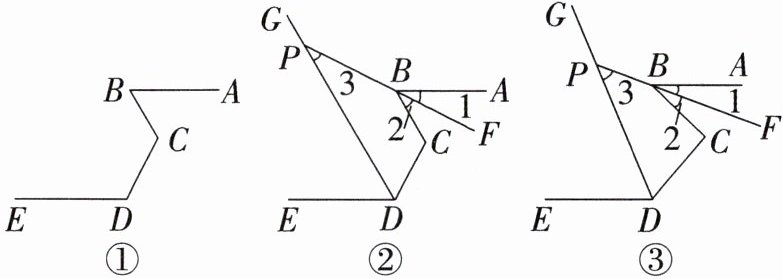
答案：
9.(1)如图①,延长DC交AB于点F,因为∠BCD + ∠BCF = 180°,∠BCF + ∠BFC + ∠FBC = 180°,所以∠BCD = ∠BFC + ∠FBC,所以∠BFC = ∠BCD - ∠ABC.因为∠CDE + ∠BCD - ∠ABC = 180°,即∠CDE + ∠BFC = 180°,所以AB//DE(同旁内角互补,两直线平行).
　　　　　

(2)①因为PD//BC,所以∠2 = ∠3.又因为∠ABC = 2∠3,∠ABC = ∠1 + ∠2,∠1 = α,所以∠1 = ∠2 = ∠3 = α,∠ABC = 2α.因为DG平分∠EDC,∠CDG + ∠C = 180°,所以 $\frac{1}{2}$∠EDC + ∠C = 180°,所以∠EDC = 360° - 2∠C.因为∠EDC + ∠BCD - ∠ABC = 180°,即∠EDC = 180° - ∠C + 2α,所以360° - 2∠C = 180° - ∠C + 2α,即∠C = 180° - 2α.
②∠1 = ∠2.理由如下:
如图②,过点C作CH平分∠BCD交DG于点H,则∠4 = ∠5 = $\frac{1}{2}$∠BCD.
因为DG平分∠EDC,所以∠CDG = $\frac{1}{2}$∠EDC,所以∠5 + ∠CDG = $\frac{1}{2}$(∠BCD + ∠EDC),又因为∠CDE + ∠BCD - ∠ABC = 180°,所以∠5 + ∠CDG = $\frac{1}{2}$(180° + ∠ABC) = 90° + $\frac{1}{2}$∠ABC,所以∠PHC = 90° + $\frac{1}{2}$∠ABC.因为∠3 + $\frac{1}{2}$∠BCD = 90°,所以∠3 + ∠4 = 90°,所以∠PBC = 360° - ∠3 - ∠4 - ∠PHC = 360° - 90° - 90° - $\frac{1}{2}$∠ABC = 180° - $\frac{1}{2}$∠ABC.又因为∠PBC + ∠2 = 180°,所以∠2 = $\frac{1}{2}$∠ABC,所以∠1 = ∠2.