2025年学霸题中题七年级数学上册苏科版第157页解析答案

1. 如图,将$∠A为30^{\circ}的直角三角尺ABC的直角顶点C$放在直尺的一边上,则$∠1 + ∠2$的度数为(

)
A.$60^{\circ}$
B.$45^{\circ}$
C.$30^{\circ}$
D.不确定

答案：1.A　解析:过点B作BD//EF交AC于点D,在直角三角尺ABC中,∠A = 30°,所以∠ABC = 60°.因为BD//EF,所以∠1 = ∠ABD.因为BD//EF,MN//EF,易证MN//BD,所以∠2 = ∠CBD,所以∠1 + ∠2 = ∠ABD + ∠CBD = ∠ABC = 60°.故选A.

2. (1)如图①,直线$l_{1}// l_{2}$,$∠A = 125^{\circ}$,$∠B = 85^{\circ}$,则$∠1 + ∠2 = $______$^{\circ}$。

(2)(菏泽中考)如图②,$AD// CE$,$∠ABC = 100^{\circ}$,则$∠2 - ∠1 = $______$^{\circ}$。

答案：
2.(1)30　解析:如图①,过点A作l₁的平行线AC,过点B作l₂的平行线BD,所以∠3 = ∠1,∠4 = ∠2.因为l₁//l₂,所以AC//BD,所以∠CAB + ∠ABD = 180°,所以∠3 + ∠4 = 125° + 85° - 180° = 30°,所以∠1 + ∠2 = 30°.
　　　

(2)80　解析:如图②,作BF//AD,因为AD//CE,易证AD//BF//EC,所以∠1 = ∠3,∠4 + ∠2 = 180°.因为∠3 + ∠4 = 100°,所以∠1 + ∠4 = 100°,所以∠2 - ∠1 = 180° - 100° = 80°.
　　一题多解
　如图②,延长AB交CE于点G,因为AD//CE,所以∠1 = ∠5.因为∠ABC = 100°,所以∠CBG = 180° - 100° = 80°.又180° - ∠2 = 180° - (∠CBG + ∠5),所以∠2 = ∠CBG + ∠5,所以∠2 - ∠5 = 80°,即∠2 - ∠1 = 80°.

3. 如图,$AB// EF$,$∠C = 90^{\circ}$,则$\alpha$,$\beta和\gamma$的关系是( )

A.$\beta = \alpha + \gamma$
B.$\alpha + \beta + \gamma = 180^{\circ}$
C.$\alpha + \beta - \gamma = 90^{\circ}$
D.$\beta + \gamma - \alpha = 180^{\circ}$

答案：
3.C　解析:延长DC交AB于点G,延长CD交EF于点H,如图,在直角三角形BGC中,∠1 = 90° - α;在三角形EHD中,∠EDH = 180° - β,∠EDH + γ + ∠2 = 180°,所以180° - β + γ + ∠2 = 180°,所以∠2 = β - γ.因为AB//EF,所以∠1 = ∠2,所以90° - α = β - γ,所以α + β - γ = 90°.故选C.
　

4. 如图,$AB// CD$,若$∠E + ∠G = ∠H$,则$∠A + ∠B + ∠C + ∠D + ∠F$的度数为______$^{\circ}$。

答案：
4.360　解析:如图所示,延长AE,DG交于点Q,过点H,Q分别作AB,CD的平行线l₁,l₂,连接FQ,由平行线的性质,易得∠A + ∠D = ∠AQD,∠B + ∠BHC + ∠C = 360°.又因为∠FEQ + ∠EFQ + ∠EQF = 180°,∠FEQ = 180° - ∠AEF,所以180° - ∠AEF + ∠EFQ + ∠EQF = 180°,所以∠EFQ + ∠EQF = ∠AEF　①.同理可得∠GFQ + ∠GQF = ∠DGF②.所以① + ②得∠EFQ + ∠EQF + ∠GFQ + ∠GQF = ∠AEF + ∠DGF,整理得∠EFG + ∠EQG = ∠AEF + ∠DGF,所以∠EQG = ∠AEF + ∠DGF - ∠EFG,所以∠A + ∠D = ∠AEF + ∠DGF - ∠EFG,即∠EFG = ∠AEF + ∠DGF - (∠A + ∠D).又因为∠AEF + ∠DGF = ∠BHC,所以∠A + ∠B + ∠C + ∠D + ∠EFG = ∠A + ∠B + ∠C + ∠D + ∠AEF + ∠DGF - (∠A + ∠D) = ∠B + ∠C + ∠BHC = 360°.
　　　　　　　　

5. 已知直线$AB// DC$,点$P$为平面上一点,连接$AP与CP$。
(1)如图①,点$P在直线AB$,$CD$之间,当$∠BAP = 60^{\circ}$,$∠DCP = 20^{\circ}$时,求$∠APC$的度数。
(2)如图②,点$P在直线AB$,$CD$之间,在$AC$左侧,$∠BAP与∠DCP的平分线相交于点K$,写出$∠AKC与∠APC$之间的数量关系,并说明理由。
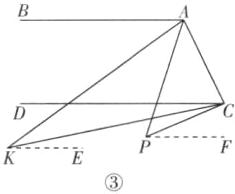
(3)如图③,点$P落在CD$外,$∠BAP与∠DCP的平分线相交于点K$,$∠AKC与∠APC$有何数量关系？并说明理由。

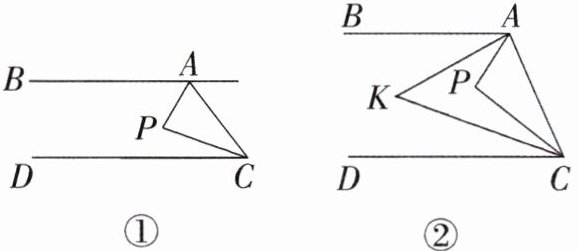
答案：
5.(1)如图①,过点P作PE//AB,因为AB//CD,所以PE//AB//CD,所以∠APE = ∠BAP,∠CPE = ∠DCP,所以∠APC = ∠APE + ∠CPE = ∠BAP + ∠DCP = 60° + 20° = 80°.
　　　　　　

(2)∠AKC = $\frac{1}{2}$∠APC.理由:如图②,过点K作KE//AB,因为AB//CD,所以KE//AB//CD,所以∠AKE = ∠BAK,∠CKE = ∠DCK,所以∠AKC = ∠AKE + ∠CKE = ∠BAK + ∠DCK.过点P作PF//AB,同理可得∠APC = ∠BAP + ∠DCP.因为∠BAP 与∠DCP 的平分线交于点K,所以∠BAK + ∠DCK = $\frac{1}{2}$∠BAP + $\frac{1}{2}$∠DCP = $\frac{1}{2}$(∠BAP + ∠DCP) = $\frac{1}{2}$∠APC,所以∠AKC = $\frac{1}{2}$∠APC.
(3)∠AKC = $\frac{1}{2}$∠APC.理由:如图③,过点K作KE//AB,因为AB//CD,所以KE//AB//CD,所以∠BAK = ∠AKE,∠DCK = ∠CKE,所以∠AKC = ∠AKE - ∠CKE = ∠BAK - ∠DCK.过点P作PF//AB,同理可得∠APC = ∠BAP - ∠DCP.因为∠BAP 与∠DCP 的平分线相交于点K,所以∠BAK - ∠DCK = $\frac{1}{2}$∠BAP - $\frac{1}{2}$∠DCP = $\frac{1}{2}$(∠BAP - ∠DCP) = $\frac{1}{2}$∠APC,所以∠AKC = $\frac{1}{2}$∠APC.
　　　　　　　　