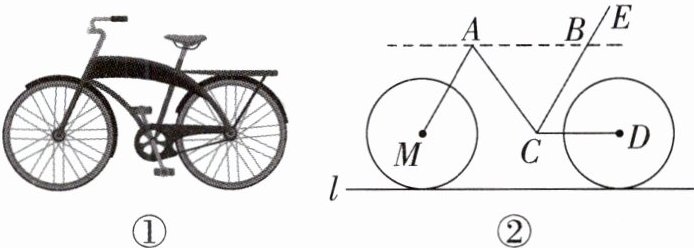
9. 新情境 (2024·南昌期中)某市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面上的实物图,图②是其示意图.其中AB,CD都与地面l平行,$∠BAC= 54^{\circ },∠BCD:∠ACB= 10:11$,当$∠MAC$为______$^{\circ }$时,AM与BC平行.
66
答案:66 解析:因为AB,CD都与地面l平行,所以AB//CD,所以∠BAC+∠ACD=180°,所以∠BAC+∠ACB+∠BCD=180°.因为∠BAC=54°,所以∠ACB+∠BCD=180°−54°=126°.因为∠BCD:∠ACB=10:11,所以∠ACB=$\frac{11}{21}$×126°=66°,所以当∠MAC=∠ACB=66°时,AM//CB.
解析:
解:∵AB,CD都与地面l平行,
∴AB//CD,
∴∠BAC+∠ACD=180°,
即∠BAC+∠ACB+∠BCD=180°,
∵∠BAC=54°,
∴∠ACB+∠BCD=180°-54°=126°,
∵∠BCD:∠ACB=10:11,
∴∠ACB=$\frac{11}{10+11}$×126°=66°,
当AM//BC时,∠MAC=∠ACB=66°,
故答案为:66。
10. 如图,已知$AC// FE,∠1+∠2= 180^{\circ }$.
(1)判断$∠FAB与∠BDC$的大小关系,并说明理由;
(2)若AC平分$∠FAD,FE⊥BE$于点E,$∠FAD= 76^{\circ }$,求$∠BCD$的度数.

答案:(1)∠FAB=∠BDC.理由:因为AC//EF,所以∠1+∠FAC=180°.因为∠1+∠2=180°,所以∠FAC=∠2,所以FA//CD,所以∠FAB=∠BDC.
(2)因为AC平分∠FAD,所以∠FAC=$\frac{1}{2}$∠FAD=$\frac{1}{2}$×76°=38°.由(1)知∠FAC=∠2,所以∠2=38°.因为AC//EF,EF⊥BE,所以∠ACB=90°,所以∠BCD=∠ACB−∠2=90°−38°=52°.
11. 新趋势 过程性学习 陈佩与小晴在讨论性质“平行于同一条直线的两条直线平行”的证明方法.
陈佩说道:“我们之前证明两条直线平行时,常在‘三线八角’的图形中进行研究.此图中没有‘三线八角’的图形,能不能构造出‘三线八角’的图形呢?”
小晴想了想,说道:“可以构造一条截线MN,与三条已有直线AB,CD,EF分别交于点H,G,K,然后就可以用平行线的判定定理进行证明了.”
按照上述同学的说法,完成证明:
已知:如图,$CD// AB,EF// AB$.
求证:$CD// EF$.
(1)在图中画出辅助线MN,并标出点H,G,K;
(2)补全证明过程.

答案:(1)如图所示.

(2)因为CD//AB,所以∠BHG=∠DGK(两直线平行,同位角相等).因为EF//AB,所以∠BHG=∠GKE(两直线平行,内错角相等),所以∠DGK=∠GKE,所以CD//EF(内错角相等,两直线平行).
技法点拨
“平行于同一条直线的两条直线平行”这个结论可在“过拐点作平行线”这类题型中运用,具体见专题22.
12. 如图,已知$AM// BN$,点P是射线AM上一动点(与点A不重合),BC,BD分别平分$∠ABP和∠PBN$,分别交射线AM于点C,D.
(1)若$∠A= 40^{\circ }$,则$∠CBD= $______$^{\circ }$.
(2)当点P运动时,$∠APB与∠ADB$之间的数量关系是否随之发生改变?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当$∠A= 2∠ABC,4∠BCM= 3∠BDC$时,求$∠A$的度数.

答案:(1)70 解析:因为AM//BN,所以∠A+∠ABN=180°.因为∠A=40°,所以∠ABN=180°−40°=140°.因为BC,BD分别平分∠ABP和∠PBN,所以∠CBP=$\frac{1}{2}$∠ABP,∠DBP=$\frac{1}{2}$∠NBP,所以∠CBD=∠CBP+∠DBP=$\frac{1}{2}$∠ABP+$\frac{1}{2}$∠NBP=$\frac{1}{2}$∠NBA=70°.
(2)不变化,∠APB=2∠ADB.理由:因为AM//BN,所以∠APB=∠PBN,∠ADB=∠DBN.因为BD平分∠PBN,所以2∠DBN=∠NBP,所以∠APB=2∠ADB.
(3)如图,延长NB至点H,设∠A=2∠ABC=2x°.因为AM//BN,所以∠ABH=∠A=2x°,∠BCM=∠CBH=3x°,∠A+∠ABN=180°,所以∠ABN=180°−2x°.
因为BC,BD分别平分∠ABP和∠PBN,所以∠ABP=2x°,∠DBN=$\frac{1}{2}$(180°−2x°−2x°)=90°−2x°.因为AM//BN,所以∠BDC=∠DBN=90°−2x°.因为4∠BCM=3∠BDC,所以4×3x°=3(90°−2x°),解得x=15,所以∠A=2x°=30°.
