1. (2024·甘孜州中考)如图,$AB// CD$,AD平分$∠BAC,∠1= 30^{\circ }$,则$∠2= $ (
B
)
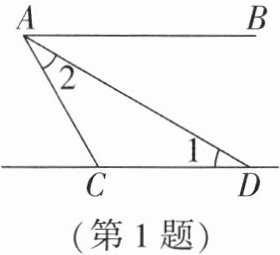
A.$15^{\circ }$
B.$30^{\circ }$
C.$45^{\circ }$
D.$60^{\circ }$
答案:B
解析:
解:∵AB//CD,∠1=30°,
∴∠BAD=∠1=30°(两直线平行,内错角相等)。
∵AD平分∠BAC,
∴∠2=∠BAD=30°。
答案:B
2. 如图,直线$AB// CD$,BC平分$∠ABD,∠1= 65^{\circ }$,则$∠2$的度数为 (
C
)
A.$25^{\circ }$
B.$40^{\circ }$
C.$50^{\circ }$
D.$65^{\circ }$
答案:C 解析:因为AB//CD,所以∠ABC=∠BCD=∠1=65°,∠ABD+∠BDC=180°.因为BC平分∠ABD,所以∠ABD=2∠ABC=130°,所以∠2=∠BDC=180°−∠ABD=180°−130°=50°.故选C.
3. 如图,在三角形ABC中,D是BC上一点,$DE// AC$,交AB于点E,$DF// AB$,交AC于点F.若$∠B+∠C= 120^{\circ }$,则$∠EDF= $ (
C
)
A.$30^{\circ }$
B.$50^{\circ }$
C.$60^{\circ }$
D.$70^{\circ }$
答案:C 解析:因为DF//AB,所以∠B=∠CDF.又因为DE//AC,所以∠C=∠BDE.因为∠B+∠C=120°,所以∠CDF+∠BDE=120°,所以∠EDF=60°.故选C.
4. (1)(2023·锦州中考改编)如图①,将一个含$45^{\circ }$角的直角三角尺按如图所示的位置摆放在直尺上.若$∠1= 28^{\circ }$,则$∠2$的度数为______$^{\circ }$.

(2)(2023·内蒙古中考改编)将一副直角三角尺按如图②所示的方式摆放,点C在FD的延长线上,且$AB// FC$,则$∠CBD$的度数为______$^{\circ }$.
答案:(1)107 解析:如图,因为∠1=28°,∠3=45°,所以∠4=180°−∠1−∠3=107°.因为直尺上下两边平行,所以∠2=∠4=107°.

(2)15 解析:因为AB//FC,所以∠ABD=∠EDF=45°.又因为∠CBD=∠ABD−∠ABC,所以∠CBD=45°−30°=15°.
5. 教材P192习题T5变式 (2023·威海中考)某些灯具的设计原理与抛物线有关.如图,从点O照射到抛物线上的光线OA,OB等反射后都沿着与直线PQ平行的方向射出.若$∠AOB= 150^{\circ },∠OBD= 90^{\circ }$,则$∠OAC= $______$^{\circ }$.

60
答案:60 解析:因为PQ//BD,∠OBD=90°,所以∠POB=90°,所以∠AOP=∠AOB−∠POB=150°−90°=60°.因为AC//PQ,所以∠OAC=∠AOP=60°.
6. 如图,直线$l_{1}// l_{2}$,直线$l_{3}交l_{1}$于点A,交$l_{2}$于点B,过点B的直线$l_{4}交l_{1}$于点C.若$∠3= 50^{\circ },∠1+∠2+∠3= 240^{\circ }$,则$∠4= $______$^{\circ }$.

答案:70 解析:如图,因为l1//l2,所以∠1+∠3=180°.因为∠1+∠2+∠3=240°,所以∠2=240°−(∠1+∠3)=60°.因为∠3+∠2+∠5=180°,∠3=50°,所以∠5=180°−∠2−∠3=70°.因为l1//l2,所以∠4=∠5=70°.

7. 新趋势 开放性试题 如图,BD平分$∠ABC,∠C= 30^{\circ },∠ABD= 75^{\circ }$,AE,BD交于点F.
(1)证明:$AB// CD$.
(2)若$AE// BC$,求
①
的度数.请从“①$∠AFD$,②$∠A$”中选择一项填在空格处(填写序号),并写出求解过程.

答案:(1)因为BD平分∠ABC,∠ABD=75°,所以∠ABC=2∠ABD=150°.因为∠C=30°,所以∠C+∠ABC=180°,所以AB//CD.
(2)填①.因为BD平分∠ABC,∠ABD=75°,所以∠DBC=∠ABD=75°.因为AE//BC,所以∠DFE=∠DBC=75°,所以∠AFD=180°−75°=105°.
填②.因为AE//BC,所以∠ABC+∠A=180°.又∠DBA=∠DBC=75°,所以∠ABC=150°,所以∠A=180°−150°=30°.
8. 如图,四边形ABCD为一长方形纸带,$AB// CD$,将ABCD沿

EF折叠,A,D两点分别与$A',D'$对应,若$∠CFE= 2∠CFD'$,则$∠AEF$的度数是 (
C
)
A.$60^{\circ }$
B.$70^{\circ }$
C.$72^{\circ }$
D.$75^{\circ }$
答案:C 解析:由翻折的性质可知∠DFE=∠D'FE.因为∠CFE=2∠CFD',设∠CFD'=x,则∠CFE=2x,∠DFE=3x,所以5x=180°,解得x=36°,所以∠DFE=3x=108°.因为AB//CD,所以∠AEF+∠DFE=180°,所以∠AEF=180°−108°=72°;故选C.