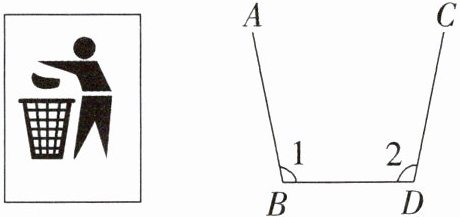
1. (2025·自贡校级月考)如图,在“垃圾入桶”标志的平面示意图中,$∠1与∠2$是一对 (
C
)
A.同位角
B.内错角
C.同旁内角
D.对顶角
答案:C 解析:直线AB,CD被直线BD所截,∠1与∠2都在两直线AB,CD之间,并且在直线BD(截线)的同旁,所以∠1与∠2是一对同旁内角.故选C.
2. (2024·西安校级模拟)下列图形中,由$∠1= ∠2$,能得到$AB// CD$的是 (
D
)

答案:D
3. 如图,不能判定$l_{1}// l_{2}$的条件是 (
D
)

A.$∠1= ∠3$
B.$∠2+∠4= 180^{\circ }$
C.$∠4= ∠5$
D.$∠2= ∠3$
答案:D 解析:A.∠1与∠3是内错角,故∠1 = ∠3可以判定l₁//l₂;B.∠2与∠4为同旁内角,故∠2 + ∠4 = 180°可以判定l₁//l₂;C.∠4与∠5为同位角,故∠4 = ∠5可以判定l₁//l₂;D.∠2 = ∠3不能判定l₁//l₂.故选D.
4. 新趋势 开放性试题 (2024·北京期中)如图,在四边形ABCD中,点F在AD的延长线上,点E在AB的延长线上,如果添加一个条件,使$AB// DC$,那么可添加的条件为
∠FDC = ∠A
. (任意添加一个符合题意的条件即可)
答案:∠FDC = ∠A(答案不唯一) 解析:当∠FDC = ∠A时,由同位角相等,两直线平行得AB//DC;当∠ADC + ∠A = 180°时,由同旁内角互补,两直线平行得AB//DC;当∠C + ∠ABC = 180°时,由同旁内角互补,两直线平行得AB//DC.(答案不唯一)
5. 如图,三块相同的三角尺(三个角的度数分别为$30^{\circ },60^{\circ },90^{\circ }$)拼成一个图形,则图中的平行线有
AB//EC,AC//ED,AE//BD
.
答案:AB//EC,AC//ED,AE//BD 解析:∠D = ∠BCA = 60°,由同位角相等,两直线平行可得AC//ED;∠BAC = ∠ACE = 90°,由内错角相等,两直线平行可得AB//EC;∠B + ∠BAE = 180°,由同旁内角互补,两直线平行可得AE//BD.
6. 教材P187练习T3变式 如图,过三角形ABC的顶点A作直线EF,K是BC边上一点,连接FK交AC边于点D,且$FD⊥AC,∠1+∠C= 90^{\circ },∠C= ∠2$,则直线AB与DF平行吗? 为什么?

答案:平行.理由:
方法一:因为∠C = ∠2,∠1 + ∠C = 90°,所以∠2 + ∠1 = 90°,所以∠BAC = 180° - 90° = 90°.因为FD⊥AC,所以∠FDA = 90°,所以∠BAC = ∠FDA,所以AB//DF(内错角相等,两直线平行).
方法二:因为∠C = ∠2,∠1 + ∠C = 90°,所以∠2 + ∠1 = 90°,所以∠BAC = 90°.因为FD⊥AC,所以∠KDA = 90°,所以∠BAC + ∠KDA = 180°,所以AB//DF(同旁内角互补,两直线平行).
方法三:因为∠C = ∠2,∠1 + ∠C = 90°,所以∠2 + ∠1 = 90°,所以∠BAC = 90°.因为FD⊥AC,所以∠KDC = 90°.所以∠BAC = ∠KDC,所以AB//DF(同位角相等,两直线平行).
7. 数学课上,老师在投影屏上展示了一个如图所示的图形,并鼓励同学们积极思考,添加一个条件,使得$DE// AC$.同学们回答完毕之后,老师在投影屏上展示了四位同学的条件,并说明其中一位同学的条件是不符合要求的,则这位同学是 (
C
)

A.甲
B.乙
C.丙
D.丁
答案:C 解析:因为∠A = ∠1,所以DE//AC,故甲不符合题意;因为∠2 + ∠4 = 180°,所以DE//AC,故乙不符合题意;因为∠A = ∠3,所以AB//DF,故丙符合题意;因为∠3 = ∠4,所以DE//AC,故丁不符合题意.故选C.